1. Deviation for a prism:

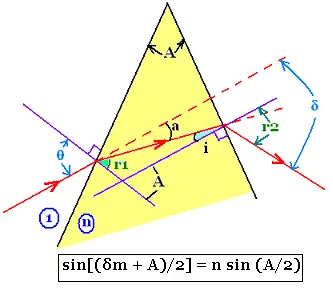
We have the five following relationships:
i + r1 = A
θ = a + r1
sin θ = n sin r1
n sin i = sin r2
δ = a + r2 - i

Then:
δ = θ - r1 + arcsin[n sin i] - i = θ + arcsin[n sin i] - A

arcsin[n sin i] = arcsin[n sin (A - r1)] = arcsin[n sin (A - arcsin (sin θ)/n)] =
Therefore:
δ = θ - A + arcsin[n sin (A - arcsin (sin θ)/n)]     (1)

The minimum deviation δ_m is determined as follows:
dδ/d θ = 0
We know that d[arcsin x ]/dx = 1/(1 - x²)^1/2
If f(x) = arcsin (x) then sin f(x) = x; and by a derivative : f'(x) cos f(x) = dx/dx = 1, therefore: f'(x) = 1/[1 - sin²f(x)]^1/2 = 1/[1 - x²]^1/2
Then:
dδ/d θ = 1 + 1/[1 - (arcsin[n sin (A - arcsin (sin θ)/n)] )²]^1/2 x n cos(A - arcsin (sin θ)/n) x {- 1/sqrt[1 - (sin θ)/n]²)^1/2} x (cosθ)/n) =

dδ/d θ = 0 leads to:
1 = 1/[1 - (arcsin[n sin (A - arcsin (sin θ)/n)] )²]^1/2 x cos(A - arcsin (sin θ)/n) x {1/sqrt[1 - (sin θ)/n]²)^1/2} x cosθ)

This equation is satisfied by the relationship:
sin θ = n sin (A/2)     (2)

2. Minimal deviation for a prism:

We have then the expression of the minimum angle of deviation : δ_m = 2 θ - A     (3)

The equation (2) becomes:
sin[(δ_m + A)/2] = n sin (A/2)     (4)

The first five relationships along with the ralationship (2) give: sin θ = n sin r1
→ r1= A/2, and i = A/2. Then i = r1
n sin i = sin r2 → n sin (A/2) = sin r2 → r2 = θ

The angle: π/2 - θ + a = π/2 - r1 = π/2 - A/2. It forms then with the bisect of angle A a right angle. Therefore, the refracted ray within the medium n is perpendicular to the bisect of angle A (then horizontal).