1. The first Law of Geomerical Optics:
When light is incident on an interface between two different media, various phenomena could occur. Light can be totaly or partially reflected, transmittef by refraction, scattered at the interface or absorbed in the medium. In Geometrical Optics, we consider the simple case of the propagation of light is rectillinear ( straight lines), media are homegeenous and transparent , interfaces are not uneven (smooth) that gives specular (regular) reflections, and no absorbtion of light by media.
2. Reflection of light:
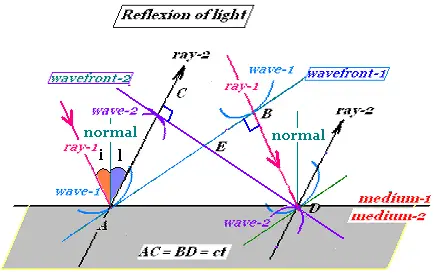
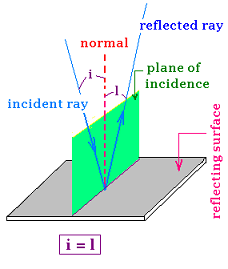
When light is incident at a plane surface, it is partially or totally reflected.
The angle of incidence (i) that the incident light ray makes with the normal at the point
of incidence is equal to the angle of reflection(r) that the reflected light ray makes
with the same normal. The incident ray, reflected ray, and normal lie in the same plane.
Using Huygen's principle, in terms of plane waves, the wavefront (wavefront-1) at the
time "0" is tangent to the wavelets wave-1 and is perpresented by the ligne "AB". When
the related left ray (ray-1) reflects from the interface at the point "A", the right
wavelet at "B" will reflects at the time "t" after. Therefore AC = BD = ct, where c
is the speed of light. At tis time "t", the right light ray "ray-1" reflects from the
point B and becomes the reflected ray "ray-2", we have a new wavefront (wavefront-2)
represented by the line CD tangent to the wavelets "wave-2".
DB is normal to AB and AC is normal to CD, because the ray is perpendicular to
its correspondant wavefront. The rectangular triangles ΔACD and ΔABD
are similar because they have two same side AC = BD = ct, and the AD is common.
Therefore, the angle <CAD and <ADB are equal.
We have:
i + l + <CAE = π/2
l + <CAE + <EAD = π/2.
Then:
i = <EAD
<EAD = π/2 - <ADB, = π/2 - <CAD
<CAD = <CAE + <EAD. Hence:
i = <EAD = π/2 - <CAE - <EAD = π/2 - <CAE - i = i + l - i = l.
We get:
i = l
The angle of incidence (i) is equal to the angle of reflection (l).