CERENKOV EFFECT

Let' consider a charged particle of velocity Vp
incident  in a transparent medium.
This particle emits photons in the "y" direction. Furthermore,
the incident charged particle recoils.





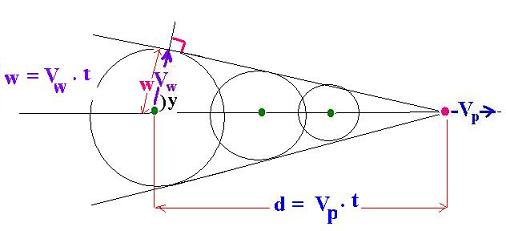
The emitted photon propagates with a speed Vw through the
medium. If the refraction index medium is n then the velocity
Vw is not equal c ( speed of light in the vacuum) but tp c/n; that is 
the speed of light in that medium. Let's write:
Vw = c/n	(1)


We consider a high-energy charged particle, that has
a velocity greater than Vw. The related Cerenkov radiation
is a chok wave.


At first, we can quickly write the following relationship, by
solving for the angle y, we have 
cos y = Vw/Vp	(2)
or cos y = c/n.Vp
We know that "y" could not exist if its cosine is
greater than 1 ( or less than -1) :
cos y = 1 gives Vp = Vw = c/n
cos y  greater than 1 : Vw greater than Vp : No radiation any more.
The threishold to have this emitted radiation is then:
Vparticule = c/n


Now, let's find the true relationship relating to cos a.
Consider the following reaction:





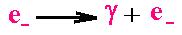
Where the electron is traveling through the medium and
gives a photon and a recoil electron.
The following figure shows the mechanism:






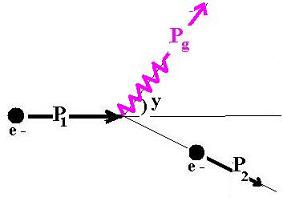
Let's do the following calculations:
Write that the liear momentum and the energy 
of this system are both concerved in the relativistic
context. We will use the following factor: 



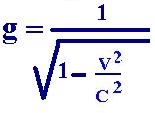with g1 = g(V1) and g2 = g(V2)
And the relation:
E0= m0c2 for the rest mass	(3)

Before the electron enters the medium 
The incident electron had:

P1 : for the liear momentum. 
E1: for the total energy, with E1 = m 1c2 	
where m1 = g1m0
Or
E12 = P12 c2 + m02c4(4)

While the electron is traveling inside the medium:


The electron has:

P2 : for the liear momentum. 
E2: for the total energy, with E2 = m 2c2 
where m2 = g2m0
Or
E22 = P22 c2 + m02c4	(5)

The photon has: 

Pg : for the liear momentum. Its magnitude is p g = hN/c
( h : Planck constant, N the frequency of the emitted radiation, and c the speed
of light in the vaccum)
Because the emitted photon  is moving through the 
medium of refraction index equal to n, we have:

pg= hN/(c/n)	(6)
Eg = hN: for its  total energy.


The conservation of the momentum is:
P1 + P2  = Pg 	(7)
hence:
P2  = Pg  - P1 
Or:
p2 2 = pg2  + p12 - 2.p1 pg cos y	(8)

The conservation of energy is:
E1 = Eg + E2
That is:
P12 c2 + m02c4 =  hN  + P22 c2 + m02c4

Using the relation (8) :
(P12 c2 + m02c4) 1/2  - hN = (g2  +  p12 - 2.p1 pg cos y + m02c4 )1/2	(9)

Hence, using (6)
cos y = (2hN.(P12 c2 + m02c4) 1/2 + ( n2 - 1)h2N2)/2c2p1p2	(10)

We have :
p1 = g1m0V1
Substituting this relation into (10), we get:
cos y = c/nV1 + (n2- 1) hN/2nc2g1m0V1

Or :

cos y = c/nV1 + ((n2 -1 ). hN  (c2 - V2)1/2  )/(2ncm02V1)
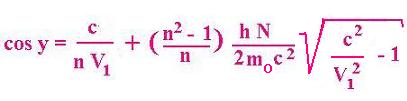