Doppler effect
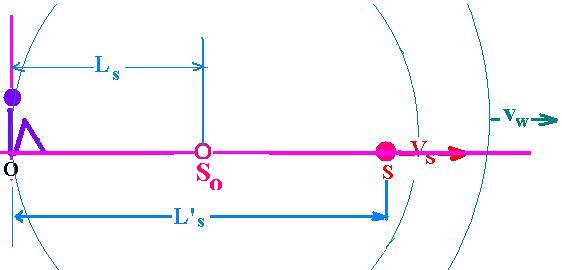
1. The Observer is at rest and the source
moves at Vs backwards the Observer
When the source S is moving forward at the speed Vs from the
observer, at the precise time T, which is the period of the wave,
this wave that was emitted from the position So reaches the observer.
The source at this time is not located at the distance So, but It
was moved and now located at the distance L's.
For the observer, It seems that the wave was originated from the
position S taking T' as time to arrive at its position:
L's = Vw . T'
We have :
Ls = Vw . T
And :
L's = Ls + Vs. T
Thus:
Vw . T '= Vw . T +Vs. T
Then:
T' = T . (Vw + Vs)/Vw
Or :
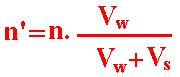
Where n' is the apparent frequency
for the Observer.
n is the real frequency of the wave.
Remarks:
- When the source is stationary (Vs =0)
then n' = n and T' = T, that is the observer
get waves at every real period.
- The more the speed Vs is big, the more the right edges
of the waves are squeezed and leaving behind distant
position between the edges. In the front , we have what we
call the sound boom or the shock wave if the wave is a sound.
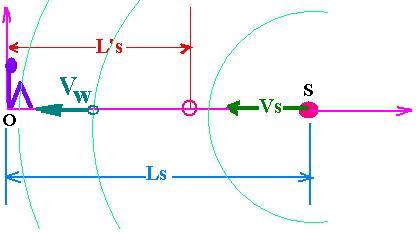
2. The Observer is at rest and the source
moves at Vs towards the Observer
Next, the observer sit down on the frame O is at rest. The source
S is moving at a speed Vs towards the Observer. The wave propagates
at the speed Vw in all directions and towards the observer of course.
When this observer receives the wave, at this precise time, the
source is located not in Ls but in L's. For the observer, the
period of the wave is T's. And at this precise time, the wave has
travelled Ls = Vs . T , where T is the real period .
T's is the apparent period.
We can write:
L's = Ls - Vs . T
Because Ls = Vw . T
and L's = Vw . T's
Thus :
Vw . T's = Vw . T - Vs . T = (Vw - Vs) . T
Or
1/T's = Vw /(Vw - Vs) (1/T)
Which means that the apparent frequency
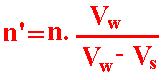
3. The Observer moves at Vo and the source at Vs
Now, let's consider that the Observer is moving
at a speed Vo and the source is moving at a speed Vs,
approaching the observer, that is in the opposite direction.
The wave is always moving at the velocity Vw.
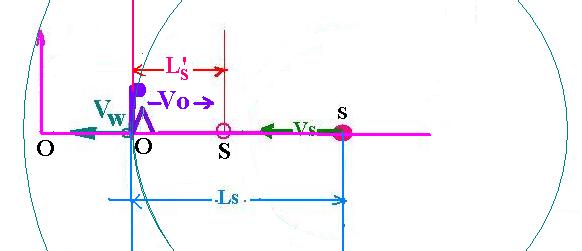
This case is like the last one except that the observer
is moving. Then instead of L's = Vw . T' , we have
L's = (Vw + Vo) . T'
Thus :
(Vw + Vo) . T' = (Vw - Vs) . T
Hence:
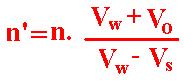
In the relativistic case, the frequency ( 1/time) could be changed into:
1/gt
Where g = 1/(1- (V2/c2))1/2
Hence :
n' ( Relativistic) = (1/g) . n ( Classic)
For the latter case, we have:
n' = n .( (Vw+Vs)/(Vw-Vs))1/2 . (Vw+Vo)/Vw
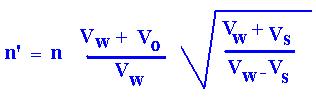
In the case of the wave is light, Vw = c ( 3.10 8m/s)
Then :
n' = n .( (c+Vs)/(c-Vs))1/2 . (c+Vo)/c
In the cast of the Observer is at rest, V0 =0, then:
n' = n .( (c+Vs)/(c-Vs))1/2 .
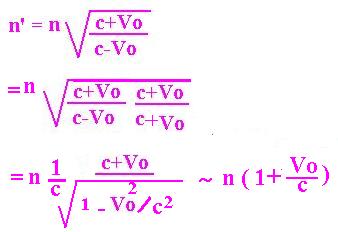
Studying Physics requires logic then Mathematics. Everything in Physics
is effects, we are just trying to find their causes.
|

