HALL effect
Let's consider the following figure:
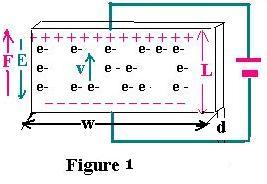
A current with intensity I flows through a conductor
with L as length, w as width and d as depth.
If v is the velocity of the travelling electron
through the distance L, then the related time is
t = L/v (1)
The expression of the current is :
I = Q/t =(N.e).Volume /t = N.e.(L.d.w ). v/L = N.e.d.w.v
N = number of electrons per volume unit
The expression of the current in the conductor is then:
I = N.e.d.w.v
Now, If the conductor is in the magnetic field, this latter exerts
a transverse force on the moving charge and pushes them to
one side of the conductor, as it is illustrated in the following figure:
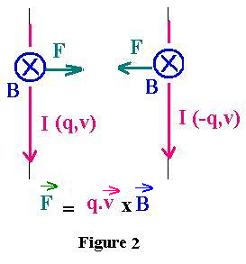
We know that the entire expression of the Lorentz force
is written as:
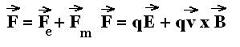
The "right-hand rule" gives the direction of the force Fm.
Now, let's see the following experiment:
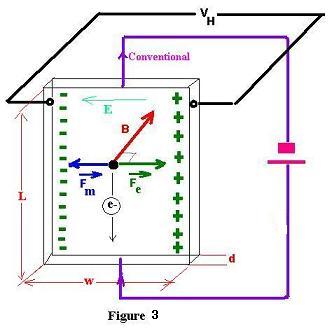
Remember that the conventional current is in the
in the opposite direction of the moving electrons.
The magnitude of the Lorentz magnetic force Fm is:
Fm = evB (2)
The magnitude of the Lorentz electric force Fe is:
Fe = eE (3)
Equating (2) and (3), we get :
E = vB (4)
The work done by the force Fe is:
W = F.w = eEw= eV (5)
Where V is the potential difference VH
The relationship (5) gives:
E = V/w (7)
Thus (3) becomes:
E = vB = V/w
Thus:
v = V/wB (8)
From the relationship (6), We have:
I =N.e.d.w. V/wB = N.e.d. V/B (9)
Then:
VH = BI /N.e.d
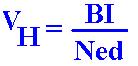
This the voltage between the two sides of the conductor.
This measurable transverse voltage is called the Hall voltage.
discovered by E. H. Hall in 1879.
We use this effect to measure a large magnetic fields on the
order of a Tesla . Commonly, we place thin film (Hall probe)
in the magnetic field the measure the transverse voltage
(some microvolts).
|

