Photoelectric effect
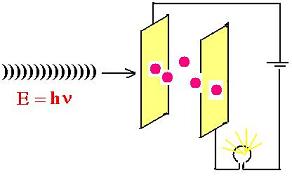
The experiment above shows photons interacting
with a metal. These photons ionize atoms, that is
kick out electrons from this atom. No other photons
will come out from the metal.
The incident photon must have a sufficient energy to
eject an bounded electron (at least this binding energy).
This is the work W to do first; otherwise, with no sufficient
energy, no electron will be emitted. The rest of energy that remains
from the incident photon is used to move the ejected electron,
that is K = (1/2)mv2. We can then write the following
formula:
E = W + K (1)
E = hν = W + (1/2) mv2
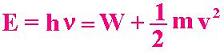 The photoelectric effect is used for x-ray and gamma
ray photons with energies below 50 keV . For energies
greater than this value, other effects become dominant.
The photoelectric effect is used for x-ray and gamma
ray photons with energies below 50 keV . For energies
greater than this value, other effects become dominant.
The photoelectric effect was discovered by Frank Hertz
in 1887. The classical theory did not have sufficient
proofs to demonstrate this effect. Planck explained
that light is a set of photons, each photon carry an energy
that is a multiple of its frequency; in other words, the incident
radiation is quantized. Einstein used the discovery of Hertz
and the theory of Planck to state the relation (1).
The main idea is that the kinetic energy of the ejected electrons
is not depending on the intensity of the incident photons. The more
the number of photons is increased , the more the number of ejected
electrons is increased , but their kinetic energy remains the same.
|

