SAGNAC effect
I. Sagnac expression: Using relative velocities
Let's consider a pulse (a photon) moving around over
a circle of radius R. It takes for it t = 2πR/c
to make a complete rotation; for instance from the
point (1) to the point (1).
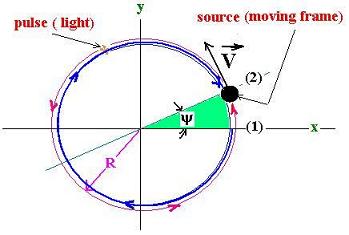
Now, let's consider that the source of light is moving
also around over the circle with the constant velocity V.
The source emits a pulse from the point (1):
We can see that if the pulse moves in the same direction
as the source, it will take to it an extra distance to
reach the source, because the source moved while it was
turning. This extra distance is the arc (1)(2).
It the pulse is emitted in the reverse direction, it will
take for the pulse less a circumference to reach the source.
the distance in less is exactly the same value of the
arc (1)(2).
For an observer "on" the moving source, there is two periods
of time for a pulse to make a complete revolution:
tcounterclockwise when the source ( and the observer)
move the same direction, and tclockwise in the reverse case.
the discrepency between these periods is the Sagnac relationship.
Let's write:
tcounterclockwise = t+
tclockwise = t-
We have:
ct+ = 2πR + arc(1)(2) = 2πR + Vt+
( We make the assumption that the angle ψ is little to consider
that the arc is a straigt line)
Solving for t+, we get:
t+ = 2πR / c-V
The same raisonning gives:
t- = 2πR / c+V
The difference in time is then:
Δt = t+ - t- = 4πRV/(c2 -V2)
If ω is the angular velocity of the source, then
V = ωR
Thus:
Δt= 4πωR2/(c2 -V2)
Or:
Δt= 4ωS/(C2 -V2)
Where S = dt = πR2, the surface of the disk.
Δt = 4ωS/(c2 -V2)
That is the Sagnac formula.
In the case of V <<c , we will have :
Δt = 4ωS/c2
II. Sagnac expression: Using mirrors
2.1 The expression of Δt
We can find the same formula by another raisonning:
Let's consider the following figure. Many mirrors are
set in the edge of the disk which is moving at the angular
velocity &omega. The angle between two consecutive mirrors
is θ:
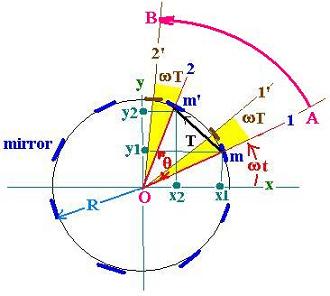
At first, at a precise time t, the pulse is sent from the first
mirror in the position (1) at ωt. The next mirror is set at
the position (2). This pulse reaches the second mirror at the time T
in the position (2') because it has moved from (2) to (2') at
the arc ωT as it did the first mirror from (1) to (1').
At the position(1); we have :
A ( x1,y1) = (Rcos(ωt), Rsin(ωt))
At the position(2'); we have :
B( x'2,y'2) = (Rcos(ωt+θ+ωT), Rsin(ωt+θ+ωT))
Let's set that θ is positive in a direction (counterclokwise)
and negative in the reverse direction (cklowise)
From (1) to (2'), the pulse traveled the distance cT, we can
write ( with the approximation that θ is small):
(cT)2 = (x'2 - x1)2 + (y'2 - y1)2
= 2R2[1 - cos(ωT + θ)]
= 2R2[1 - cos(ωT)cos(θ) + sin (ωT)sin(θ)]
Let's use the first term for sine and the two first terms
for cosine in their developement:
sin(ωT) = ωT
cos(ωT) = 1- (ωT)2/2
Thus:
(cT)2 = 2R2[1- (1- (ωT)2/2)cos(θ) + (ωT)sin(θ)]
Solving for T, we get:
[c2 - R2ω2cos(θ)]T2 - [2R2ωsin(θ)]T - 2R2( 1- cos(θ)) = 0
This equation has two solutions t1 and t2, one is
positive, the second is negative. We are interested in the sum of these solutions,
that is in the discrepency Δ(t) related to the time taken by the pulse to
travel in the two direction ( + θ and - θ).
We know that if:
ax2 + bx +c =0
then - b/a is the sum of the two solutions, hence:
Δ(θ) = [2R2ωsin(θ)] / (c2 - R2ω2cos(θ))
2.2 Results for the elementary triangle
Let's calculate S(θ), the surface of the small triangle (mOm').
We have:
s(θ) = 2.s(θ/2) = 2.(1/2).R.sin (θ/2).R.cos (θ/2) = 2R2sin(θ/2)cos(θ/2)
We know that sin(2x) = 2 sin(x)cos(x)
Thus:
s(θ) = (R2/2) sin(θ)
Let's write that θ is equal to 2π/n
where n is the number of sectors in the disk.
Thus:
s(θ) = s(n) = (R2/2) sin(2π/n)
And the entire surface S of the disk is:
S = Σs(n) = n.(R2/2) sin(2π/n) = n.s(n)
The best result is expected with the limit of S when n tends
towards ∞.
Let's write 2π/n = N
Thus:
S = 2π(R2/2)limit [(sin(N)/N] when N tends to 0 .
( the term between the brakets tends towards 1), therfore;
S = 2πR2/2 = πR2
2.3 Results for the disk
We have:
Δ(θ) = Δ(n) = [2R2ωsin(2π/n)] / (c2 - R2ω2cos(2π/n))
= 4.s(n)ω/ (c2 - R2ω2cos(2π/n))
Δ(t) = ΣΔ(θ) = ΣΔ(n) = nΔ(n)
= 4.n.s(n)ω/ (c2 - R2ω2cos2π/n))
With n tending towards ∞
cos(π/n) = 1 , and
S = πR2
Then:
Δ(t) = 4.ωS/(c2 - R2ω2)
Δ(t) = 4.ωS/(c2 - V2)
In the case of V <<c , we will have :
Δt = 4ωS/c2
Wich is the same result found as before witout using c+V or c-V.
We can state then that for the observer outside the disk,
the speed of the pulse is c+V and c-V according the two
directions and c is the speed of light even if the motion
is circular.
|

