Dirac equation: free particle

1. Dirac's equation

The main idea is to change the D'Alembertian operator in Klein_Gordon equation into a Lorentz invariant.

Here is Klein-Gordon equation is:

(1/c²)∂²/∂t²ψ - ∇²ψ + (m_o²c²/ħ²)ψ = 0

or
☐ψ + (m_oc/ħ)²ψ = 0

where
☐ = (1/c²)∂²/∂t² - ∇²


Like a 4-Vector, the wave function ψ(r,t) for which will be applied the square root of the D'Alembertian must have 4 components. Therefore, this square root of the D'Alembertian will be transformed by matrices.

Dirac factorised the d'Alembertian as follows:

∇² = - (1/c²)∂²/∂t²
= (A∂/∂x + B∂/∂y + C∂/∂z + (i/c)D∂/∂t) (A∂/∂x + B∂/∂y + C∂/∂z + (i/c)D∂/∂t)

The cross-terms of the operator A, B, C, and D will vanish, and their square must be equal to the operator indentity I. That is:
Their anticommutators {X,Y} = 0 and X² = Y² = I. (X and Y are any operator A, B, C, or D).

Hence, the Klein_gordon equation:
☐ψ + (m_oc/ħ)²ψ = 0
becomes:

[∇² - (1/c²)∂²/∂t²]ψ = (m_oc/ħ)²ψ
Or
(A∂/∂x + B∂/∂y + C∂/∂z + (i/c)D∂/∂t) ψ = (m_oc/ħ) ψ

Let's set:

A = iβα₁, B = iβα₂ , C = iβα₃, and D = β

The above equation becomes:
iβ [(α₁∂/∂x + α₂∂/∂y + α₃∂/∂z + (1/c)∂/∂t)] ψ = (m_oc/ħ) ψ

Using the symbol ∇ of the gradient operator with
the vector matrix α = (α₁, α₂, α₃), we get:

iβ [α.∇ + (1/c)∂/∂t)] ψ = (m_oc/ħ) ψ

Multiplying the both sides by ħc, we get:

[iβħc α.∇ + iħ β ∂/∂t)] ψ = (m_oc²) ψ

Since β² = 1, we have:
[iħc α.∇ + iħ∂/∂t)] ψ = (βm_oc²) ψ

Using the quantum expression of momentum operator P = -iħ∇, we get:
[- c α.P + iħ∂/∂t)] ψ = (βm_oc²) ψ

We find finally the equation:

(iħ∂/∂t) ψ = (cα.P + βm_oc²) ψ

That is the Dirac equation.


Dirac equation:
(iħ∂/∂t) ψ = (c α.P + βm_oc²) ψ
α₁, α₂, α₃, and β are 4x4 matrices.

2. Dirac's matrices

Dirac defined the matrices α₁, α₂, α₃, and β as the following:

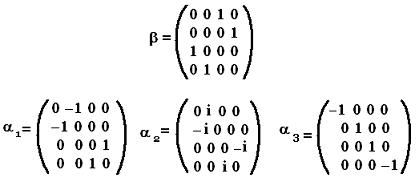
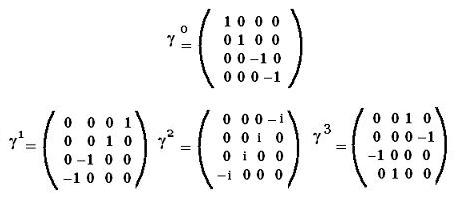
2. γ-Dirac's matrices

More better, new matrices, known as the gamma matrices are defined:
γ⁰ = β
γⁱ = β αⁱ,
i = 1, 2, 3.



Dirac Equation becomes;
(iħγ⁰∂/∂t) ψ = (c γ.P + m_oc²) ψ


(iħγ⁰∂/∂t) ψ = (c γ.P + m_oc²) ψ

Using the Pauli's matrices:



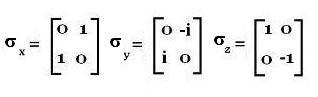
we can write:
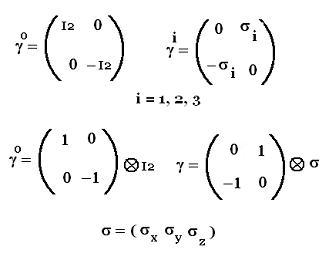