elliptic coordinates

Quantum Mechanics enables us to understands the existence and properties of chemical bonds that are responsible for the formation of molecules from isolated atoms. The simplest molecule possible is the H₂⁺ ion, which is composed of two protons and a single electron.

ρ = R/a_o
ρ₁= r₁/a_o
ρ₂= r₂/a_o


R is the internuclear distance P₂ nad P₂

The normalized gound state wave function 1s of the hydrogen atom formed around P₁ is:
φ₁ = 1/(πa_o³)^1/2 exp{- ρ₁}

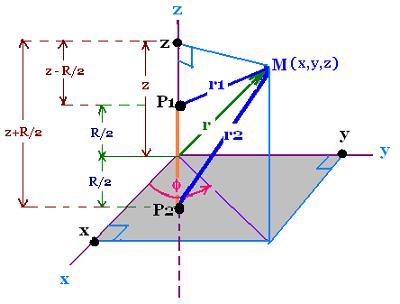
It is convenient to use the system of elliptic coordinates. The point Mof space (electron) is defined by:
μ = (r₁ + r₂)/R = (ρ₁ + ρ₂)/ρ
ν = = (r₁ - r₂)/R = (ρ₁ - ρ₂)/ρ

r₁² = x² + y² + (z - R/2)²
r₂² = x² = Y² = (z + R/2)²
tan φ = y/x

We will calculate the Jacobian of the transformation: {x,y,z} → {μ, ν, φ}; in order to write:
d³r = dxdydz = J dμdνdφ
It is more easy to calculate first J^-1, then set J according to JJ^-1 = 1.

Therefore:
∂μ/∂x = (1/R) (∂r₁/∂x + ∂r₂/∂x ) = (1/R) (x/r₁ + x/r₂) = μx/r₁r₂
∂ν/∂x = (1/R) (∂r₁/∂x - ∂r₂/∂x ) = (1/R) (x/r₁ - x/r₂) = - νx/r₁r₂
∂μ/∂y = μy/r₁r₂
∂ν/∂y = - νy/r₁r₂
∂μ/∂z = (1/R) (∂r_1/∂z + ∂r₂/∂z ) = (1/R) ((z - R/2)r₁ + (z + R/2)/r₂) = (μz + νR/2)/r₁r₂
∂ν/∂z = (1/R) (∂r_1/∂z - ∂r₂/∂z ) =
(1/R) ((z - R/2)r₁ - (z + R/2)/r₂) = - (νz + μR/2)/r₁r₂
∂φ/∂x = - y/(x² + y²)
∂φ/∂y = x/(x² + y²)
∂φ/∂z = 0

Therefore:
J^-1 = (1/(r₁r₂)²)
| μx μy μz + νR/2|
|- νx - νy - (νz + μR/2)|
|- y/(x² + y²) x/(x² + y²) 0|


= μx (νz + μR/2)(x/(x² + y²)) + μy (νz + μR/2)(y/(x² + y²)) - (μz + νR/2) =
(R/2)(μ² - ν²). Then:
J^-1 = (R/2)(μ² - ν²) (1/(r₁r₂)²)
Since
μ² - ν² = 4r₁r₂/R², we have then:
(r₁r₂)² = R⁴(μ² - ν²)²/16
Hence:
J^-1 = 8/R³(μ² - ν²)
Then:
J = R³(μ² - ν²)/8

<φ₁,φ₂ > =
∫∫ d³r φ₁^* (r)φ₂ (r) = (1/πa_o³) ∫∫∫ d³r exp{-( r₁ + r₂)/a_o}
= (1/πa_o³) ∫∫∫ J dμdνdφ exp{- μρ}

We have:
μ = (r₁ + r₂)/R
μ_min = R/R = 1
μ_max = ∞/R = ∞

And
ν = (r₁ - r₂)/R
ν_min = -R/R = -1
ν_max = R/R = 1;

Then:
<φ₁,φ₂ > = (R³/8)(1/πa_o³) ∫∫∫ (μ² - ν²) dμdνdφ exp{- μρ}
[μ: 1 → ∞, ν: -1 → +1, φ: 0 → 2π ]
= 2π(R³/8)(1/πa_o³) ∫∫(μ² - ν²) dμdν exp{- μρ}
[μ: 1 → ∞, ν: -1 → +1,]
Using ρ = R/a_o yields: R³ = ρ³a_o ³ = ρ³/4

<φ₁,φ₂ > =
ρ³/4[ ∫ dμ exp{- μρ} ∫(μ² - ν²) dν]
[μ: 1 → ∞, ν: -1 → +1,]

= ρ³/4 [ ∫ dμ exp{- μρ} (2μ² - 2/3) ]
[μ: 1 → ∞]

= ρ³/2 [ ∫ dμ exp{- μρ} (μ² - 1/3)]
[μ: 1 → ∞]

= ρ³/2 [ ∫ dμ exp{- μρ} μ² - 1/3 ∫ dμexp{- μρ}]
[μ: 1 → ∞]

= ρ³/2 [ (exp{- ρμ}/ρ) [- μ² - 2 [(μ/ρ) + (1/ρ²)]] +( 1/3ρ) exp{- μρ}]
[μ: 1 → ∞]

= ρ³/2 [ (exp{- ρμ}/ρ) [- μ² - 2 [(μ/ρ) + (1/ρ²)] + 1/3]]
[μ: 1 → ∞]

= ρ³/2 [ (exp{- ρ}/ρ) [ 1 + 2 [(1/ρ) + (1/ρ²)] - 1/3]]
= ρ³/2 (exp{- ρ}/ρ) [2/3 + 2/ρ + 2/ρ²]
= ρ² (exp{- ρ}) [1/3 + 1/ρ + 1/ρ²]
= exp{- ρ} (ρ²/3 + ρ + 1)

--------------
I = ρ²E_I ∫∫∫dμdν(μ + ν) exp{-(μ + ν)ρ} dφ [μ: 1 → ∞, ν: -1 → +1, φ: 0 → 2π ] Let's write:
x = ρμ and y = ρν

I = (E_I/ρ) ∫∫dx;dy;(x + y) exp{-(x + y)}
[x: ρ → ∞, y: -ρ → +ρ ]

I = I = (E_I/ρ) J

J = ∫∫dx;dy;(x + y) exp{-(x + y)} = ∫ exp{-(x} dx; ∫dy;(x + y) exp{- y}
[x: ρ → ∞, y: -ρ → +ρ ]
J = ∫ exp{-(x} dx; K

K = ∫dy;(x + y) exp{- y} = x ∫dy; exp{- y} + ∫dy;y exp{- y} =
[y: -ρ → +ρ ]

- x exp{- y} - y exp{- y} - exp{- y} = exp{- y}[ - x - y - 1} [y: -ρ → +ρ ]
=
exp{- ρ}[ - x - ρ - 1} + exp{ ρ }[ x - ρ + 1 } =
= exp{- ρ}[ - x - ρ - 1} + exp{ ρ }[ x - ρ + 1 }
x(exp{ρ} - exp{- ρ}) - exp{- ρ}[ + ρ + 1] + exp{ ρ }[ - ρ + 1 ]
= x A + B


A = exp{ρ} - exp{- ρ}
B = - exp{- ρ}[ + ρ + 1] + exp{ ρ }[ - ρ + 1 ]
A + B = exp{ ρ }[- ρ + 1 + 1] - exp{- ρ}[ + ρ + 1 + 1] =
exp{ ρ }[- ρ + 2] - exp{- ρ}[ + ρ + 2]

J = ∫exp{-(x} dx; (xA + B)
[x: ρ → ∞,]
= A ∫exp{-(x} x dx; + B ∫exp{-(x}dx; =
[x: ρ → ∞]

A(- x exp{-x} - exp{-x}) - B exp{-(x} = exp{-(x} [- xA - A -B ]
[x: ρ → ∞]

= exp{-(ρ} [ρA + A + B] =
exp{-(ρ} [ρ(exp{ρ} - exp{- ρ}) + exp{ ρ }[- ρ + 2] - exp{- ρ}[ + ρ + 2] ] = ρ(1 - exp{- 2ρ}) + [- ρ + 2] - exp{- 2ρ}[ + ρ + 2] =
- ρexp{- 2ρ} + 2 - exp{- 2ρ}[ + ρ + 2] = exp{- 2ρ} [- 2ρ - 2] + 2 = 2 [1 - (ρ + 1) exp{- 2ρ}]
Therefore:
I = (E_I/ρ) 2 [1 - (ρ + 1) exp{- 2ρ}] =
(2E_I/ρ) [1 - (ρ + 1) exp{- 2ρ}]

x exp{-x} = x / exp{x}

lim x exp{-x} = ∞/∞ :indetermined.
x → + ∞
De l'Hopital theorem:


lim x exp{-x} = lim x / exp{x} = lim 1/ exp{x} = 0
x → + ∞

<φ₁|e²/r₁|φ₂> = e² ∫∫∫ φ₁^*(r₁)(1/r₁) φ₂(r₂) d³r

We have:
φ₁(r₁)= (1/πa_o³)^1/2exp{-ρ₁}
φ₂(r₂)= (1/πa_o³)^1/2exp{-ρ₂}
r₁ = ρ a_o(μ + ν)/2
ρ = R/a_o
∫dφ = 2π
ρ₁ + ρ₂ = μρ
J = [R³/8] (μ² - ν²)
= [(ρ a_o)³/8] (μ² - ν²)
E_I = e²/2a_o

Therefore:
<φ₁|e²/r₁|φ₂> =
e² (1/πa_o³) [(ρ a_o)³/8] (2/ρa_o) 2π ∫∫exp{-μρ} (1/(μ + ν))(μ² - ν²) dμdν =
[μ: 1 → ∞, ν: -1 → +1]


(ρ)²E_I ∫∫ exp{- μρ}(μ - ν) dμdν =
[μ: 1 → ∞, ν: -1 → +1]

(ρ)²E_I ∫exp{- μρ}dμ ∫ (μ - ν) dν =
[μ: 1 → ∞, ν: -1 → +1]
=
(ρ)²E_I ∫exp{- μρ}dμ (μ 2 - 0) =
[μ: 1 → ∞]

(ρ)²E_I 2 ∫exp{- μρ}dμ = (2/ρ²)[- μρ - 1]exp{- μρ}
[μ: 1 → ∞]

= (ρ)²E_I (2/ρ²)[ ρ + 1]exp{- ρ}

Hence:
<φ₁|e²/r₁|φ₂> = 2E_I [ρ + 1] exp{- ρ}