Fermi's golden rule

1. Transition probability between two states

Given a Hamiltonian
H(t) = H = H0 + V(t)
With 
V(t) = 0 if t<= t0
V(t) = V(t) if t> t0

If |i> are the eigenstates of H0, then:
H0 |i> = Ei |i>

Let's consider the system in the state |i> = |φ(t0)>;
at the time t0, so at a later time "t", it is 
in the state |φs(t)> = Σ cf(t)|f>

The transition probability from |i> to |f> 
is equal to |cf(t)|2.

We have:
|φs>(t); = Us(t,t0)|i> so
<f|φ>(t); = <f|Σ cf(t)|f> = cf(t) 

Hence:
cf(t)  = <f|φs(t)> = <f|Us(t,t0)|i> = 

<f|exp{- iH0(t - t0)/ℏ}Ui(t,t0)|i>
Therefore:

|cf(t)|2 = |<f|Ui(t,t0)|i>|2

We already know:

Ui(t,t0) = exp {- (i/ℏ) ∫ Hint(τ) dτ}
from t0 to t.

Then:
|cf(t)|2 = |<f|exp {- (i/ℏ) ∫ Vi(τ) dτ}|i>|2

Therefore, at the first order:
Ui(t,t0) = 1  - (i/ℏ) ∫ Vi(τ) dτ 
from t0 to t.

Then:
<f|Ui(t,t0)|i> = - (i/ℏ) ∫ <f|Vi(τ)|i> dτ 
from t0 to t.

Recall: Vi(t) = exp{ iH0(t - t0)/ℏ}V(t)exp{- iH0(t - t0)/ℏ}, so:
<f|Ui(t,t0)|i> = - (i/ℏ) ∫ dτ  <f|V(τ)|i> exp {i(Ef - Ei)(τ - t0)/ℏ} 
from t0 to t.

Pi → f = |- (i/ℏ) ∫ dτ <f|V(τ)|i> exp {i(Ef - Ei)(τ - t0)/ℏ}|2  
(τ: from t0 to t)

This is the transition probability of observing 
the system in the target state |f> prepared in the 
state |i> at time t, due to V(t).

This formula is known as the  
state-to-state form- Fermi’s Golden Rule 

2. Applications:

2.1. Time-independent perturbation:

V (t) = 0 if t <= 0
V (t) = V  if t > 0 (independent of time)

We have in this case:
Pi → f = |- (i<f|V|i>/ℏ) ∫ dτ  exp {i(Ef - Ei)(τ)/ℏ}|2  (τ: from t0 = 0 to t)

∫ dτ  exp {i(Ef - Ei)(τ)/ℏ} = (ℏ/i)(Ef - Ei) [exp {i(Ef - Ei)t/ℏ} - 1]


1 - exp{ix} = 1 - cos x - i sin x
|1 - exp{ix}|2 = (1 - cos x - i sin x)(1 - cos x + i sin x) = 
(1 - cos x)2 + sin2 x = 2 - 2 cos x  = 2 (1 - cos x)  = 4 sin2(x/2).


Then:
Pi → f = [4 |<f|V|i>|2/(Ef - Ei)2] sin2[(Ef - Ei)t/2ℏ]

Let's write: Ef - Ei = ℏ ω, so
Pi → f = [4 |<f|V|i>|2/ℏ2ω2] sin2[(ωt/2]

Now, let's write:
Pi → f = [ |<f|V|i>|2/ℏ2] f(ω)
and then set some properties of this function: 
f(ω) = (4/ω2) sin2[(ωt/2]

1. lim f(ω) = t2
when fω → 0)

2. f(ω) = 0 if ωt/2 = kπ , that is ω = 2πk/t. 
the max of the function is at ωt = 0. The first minimum is 
at ω = 2π/t. Therefore the measure of this probability 
is appreciable if  ω < 2π/t or 
ω < 2π/Δt. or ΔE Δt >=0 2πℏ, 
E Δt = Ef - Ei. And we recognize in ΔE >=0 2πℏ/Δt 
the incertainty principle.


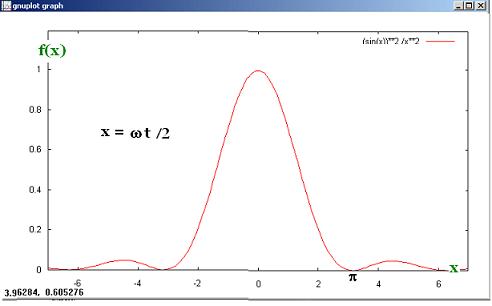gnuplot> set xrange [ 0 : 7 ]
gnuplot> set yrange [ 0 : 1.5 ]
gnuplot> plot (sin(x))**2/x**2

2.2. Time-independent perturbation at an infinite time

Now we want to set the formula for t that tends touward ∞, 
that is:
lim Pi → f = [4 |<f|V|i>|2/ℏ2ω2] sin2[(ωt/2]
t → ∞

We know 
∫ dx sin2(x)/x2 = π
x: - ∞ → +∞

Let's write:
∫ dx sin2(x)/x2 g(0) = πg(0)
- ∞ → + ∞
g is a function that we are going to determine.
Let x = ωt, so:
πg(0) = ∫ dx sin2(x)/x2 g(0) = 
=
lim ∫ dx sin2(x)/x2 g(ω) 
x:- ∞ → + &infin
t → ∞ or ω → 0 
= 
lim   ∫ (1/t)dω sin2(ωt)/ω2 g(ω) 
x:- ∞ → + &infin
t → ∞ or ω → 0
=
∫ lim (1/t)  sin2(ωt)/ω2 g(ω) dω
x:- ∞ → + &infin
t → ∞ or ω → 0

Rewriting the equation gives:

∫ lim (1/t)  sin2(ωt)/ω2 g(ω) dω = πg(0)
x:- ∞ → + &infin
t → ∞ or ω → 0

This equality is valid only if:
 lim (1/t)  sin2(ωt)/ω2 = πδ(ω)
according to the property of Dirac function wich is:
∫f(x) δ(x - a) = h(a)
x:- ∞ → + ∞ 

Thus:
lim (1/t)  sin2(ωt)/ω2 = πδ(ω)
as we see:
∫ πδ(ω) g(ω) dω = πg(0)
x:- ∞ → + ∞

Our probability, at t → + ∞ becomes:
lim Pi → f = [4 |<f|V|i>|2/ℏ2] sin2[(ωt/2]  / ω2
t → ∞
= [4 |<f|V|i>|2/ℏ2] (t/2) π 2/ℏ δ(Ef - Ei)
(We have replaced t by t/2 and use a property of δ function: 
δ(ax) = (1/a) δ(x)

Therefore:
The probability of transition from |i> to |f>, by 
unit of time (transition rate) is:

Pi → f = (2 π/ℏ) |<f|V|i>|2 δ(Ef - Ei)

2.3. Time-dependent perturbation

If V(t) is given by:
V(t) = 0 if t<= 0
V(t) = V exp{iωt} + V+exp{-iωt} if t> 0
Called armonic perturbations

we will have:
P i → f = |- i/ℏ ∫ dτ exp{i(Ef - Ei)τ/ℏ} [<f|V|i> exp{iωτ} + 
<f|V+|i> exp{-iωτ}] |2
from to to t
= |[1 - exp{-i((Ef - Ei)/ℏ + ω)t}/ ((Ef - Ei + ℏω)  f|V|i> + 
[1 - exp{-i((Ef - Ei)/ℏ - ω)t}/ ((Ef - Ei - ℏω)  f|V+|i>|2
That leads to: 

Pi → f = (2 π/ℏ) |<f|V|i>|2 δ(Ef - Ei + ℏω) +  
(2 π/ℏ) |<f|V+|i>|2 δ(Ef - Ei - ℏω)


If Ef > Ei there is absorption (energy uptake), 
then only the 2nd term contributes
If Ef < Ei there is emission (energy loss), 
then only the 1st term contributes

3. Distribution of final states

The first-order term that we have used in 
Ui(t,t0) = exp {- (i/ℏ) ∫ Hint(τ) dτ}
from t0 to t.
allows only direct transitions between
|i> and |f> . The second-order term 
accounts for transitions occuring through 
all possible intermediate states of |f>

We don’t have strictly real monochromatic light, but a frequency
spectrum of ω.Therefore, we use the radiation density. 
We use also the term Density of states &ro;(Ef).

The last version of the Fermi's golden rule becomes: 

P(i→f) = Σ(f) Pi → f = (2 π/ℏ) |<f|V|i>|2 δ(Ef - Ei)
= ∫  ρ(Ef) dEf [Pi → f]


P(i→f) = ∫ρ(Ef) dEf [Pi → f]