Quantum Mechanics
Schrodinger equation
Quantum Mechanics
Propagators : Pg
Quantum Simple Harmonic
Oscillator QSHO
Quantum Mechanics
Simulation With GNU Octave
© The scientific sentence. 2010
|
|
LCAO - hydrogen molecule H2 +
1. LCAO
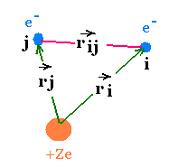
Let's consider an atom with many electrons. Each electron "i" has its kinetic energy
Ki = - ħ2/2mi and its potential energy V(ri)
= - Ze2/ri,where ri is vector position of the electron "i".
Hiφi = Ei φi
Each electron has its proper Hamiltonian Hi= Ki + V(ri),
then its wavefunction φi, and its corresponding energy Ei.
The whole system has an hamiltonian H, a wavefunction ψ and energy E, so
Hψ = E ψ
H = Σ Hi + Σ V(ri<j), where V(rij) is the
potential interaction of the electron i with another electron "j", and rij is the
vector between the electron"i" and the electron "j".
Hψ = E ψ
In the case of a molecule, we add the potential energy of each electron with each
other nucleus ans the potential interaction between nuclei. We will determine
the energy levels of the simplest mlecule, the ion diatomic hydrogen molecule
H+2, using the Born approximation, that is the nuclei
are more (1836 times) heavy than electrons and then are fixed.
Based on the fundamental principle of quantum mechanics, i.e. the wavefunction of a system can be described as a linear combination of its eigenstates, we introduce and use The LCAO = Linear Combination of Atomic Orbitals principle to describe molecular orbitals as a linear combination of atomic orbitals.
We write:
Molecular orbital : ψ
Atomic orbitals : φi
ψ = Σ ci φi
ψ = Σ ci φi
2. Ion Hydrogen molecule H2+
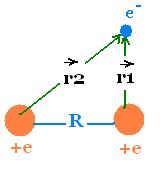
The Schrodinger equation for this system is:
Hψ = E ψ
Where:
H = K + V(r1) + V(r2 ) + V(R) =
-(ħ2/2m)∂2/∂r2 - e2/r1
- e2/r2 + e2/R
(r is the position vector of the electron from any point
as origin).
We have:
ψ = Σ ci φi =
c1 φ1 + c2 φ2
Rewriting Hψ = E ψ gives:
H (c1 φ1 + c2 φ2) = E(c1 φ1 + c2 φ2)
H (c1 φ1 + c2 φ2) =
c1 H φ1 + c2 H φ2
The component of H are given by:
<ψ*|H|ψ> = E <ψ*|ψ> =
E ∫ψ*ψdV
Therefore:
Using at left the bra: <φ*1|, we have:
c1<φ*1|H| φ1> + c2 <φ*1|H| φ2> =
E(c1 <φ*1|φ1> + c2 <φ*1|φ2>)
(1)
Similarly,
Using at left the bra: <φ*2|, we have:
c1<φ*2|H| φ1> + c2 <φ*2|H| φ2> =
E(c1 <φ*2|φ1> + c2 <φ*2|φ2>)
(2)
Now, let's write:
H11 = <φ*1|H| φ1> =
∫φ*1Hφ1 dV
H12 = <φ*1|H| φ2> =
∫φ*1Hφ2 dV
H21 = <φ*2|H| φ1> =
∫φ*2Hφ1 dV
H22 = <φ*2|H| φ2> =
∫φ*2Hφ2 dV
And:
S11 = <φ*1|φ1> =
∫φ*1φ1 dV
S12 = <φ*1|φ2> =
∫φ*1φ2 dV
S21 = <φ*2|φ1> =
∫ φ*2φ1dV
S22 = <φ*2|φ2> =
∫ φ*1φ2dV
The equation (1) and (2) become:
c1H11 + c2 H12 = E(c1 S11 + c2 S12)
(1')
c1H21 + c2 H22 = E(c1 S21 + c2 S22)
(2')
Or:
c1(H11 - ES11) + c2(H12 - ES12) = 0
c1(H21 - ES21) + c2(H22 - ES22) = 0
c1(H11 - ES11) + c2(H12 - ES12) = 0
c1(H21 - ES21) + c2(H22 - ES22) = 0
Since the molecule is symetrical, we have:
H11 = H22 and
H12 = H21
S11 = S22 and
S12 = S21
Therefore:
c1(H11 - ES11) + c2(H12 - ES12) = 0 (3)
c1(H12 - ES12) + c2(H11 - ES11) = 0 (4)
Solving for E gives:
(H11 - ES11)/ (H12 - ES12) =
(H12 - ES12) / (H11 - ES11)
(H11 - ES11)2 = (H12 - ES12)2
That is:
H11 - ES11 = + (H12 - ES12) and
H11 - ES11 = - (H12 - ES12)
E- = (H11 - H12)/(S11 - S12)
E+ = (H11 + H12)/(S11+ S12)
We obtain then the following expressions for the energies of the molecule:
E- = (H11 - H12)/(S11 - S12)
E+ = (H11 + H12)/(S11+ S12)
Substituting these values of energies in the equations (1') and (2') gives:
With E- :
c1H11 + c2H12 =
E[c1S11 + c2S12]
(S11 - S12)(c1H11 + c2H12) =
(H11 - H12)(c1S11+ c2S12)
We find:
c1 = - c2
Similarly, with E+:, we find:
c1 = + c2
Therefore, the wavefunction ψ takes two values:
ψ+ = c1(φ1 + φ2), and
ψ- = c2(φ1 - φ2)
Now, we normalize the wavefunctions ψ+ and ψ-:
<ψ+ |ψ+ > = ∫ ψ+ * ψ+ dV = 1. That is:
c12 ∫ φ1* φ dV + c22 ∫ φ2* φ2 dV + 2c12 ∫ φ1* φ2 dV
= 2 c12 [S11 + S12] = 1
Therefore:
c1 = 1/[2(S11 + S12)]1/2
Similarly,
c2 = 1/[2(S11 - S12)]1/2
The two wavefunctions ψ+ and ψ- are:
ψ+ = (φ1 + φ2)/[2(S11 + S12)]1/2
ψ- = (φ1 - φ2)/[2(S11 - S12)]1/2
The Hamiltonian operator of the molecule H2+ is:
H = -(#&295;2/2m)∂2/∂r12 - e2/r1 - e2/r2 + e2/R
The two first terms give:
(-(#&295;2/2m)∂2/∂r12 - e2/r1)φ = E1 φ
Where E1 = -13.6 (eV)/nn=1 = -13.6 (eV)
E1 = EI = e2/2ao is the ionisation energy of the hydrogen atom. ao is the Bohr radius.
Now, we will determine the diagonal Hamiltonian integral H11 = H22 called coulomb integrals, H12 = H21, called resonance integrals, and S11 = S22, and S12 = S21, called overlap integrals.
Remark that if the wavefunctions φ1 and φ1 are orthonormal, the overlap integrals become equal to the Kronecker delta, Sij = δij.
H11 = ∫φ1*Hφ1dV = E1S11 + J
where J =
∫φ1*[- e2/r2 + e2/R]φ1dV =
- ∫φ1*[e2/r2]φ1dV + e2S11/R
H12 = ∫φ1*Hφ2dV = E1S12 + K
Where K =
∫φ1*[- e2/r2 + e2/R]φ2dV =
- ∫φ1*[e2/r2]φ2dV + e2S12/R
Therefore:
H11 = E1S11 + J
H12 = E1S12 + K
And:
E- = E1 - (J - K)/(S11 - S12)
E+ = E1 + (J + K)/(S11+ S12)
E- = E1 - (J - K)/(S11 - S12)
E+ = E1 + (J + K)/(S11+ S12)
For 1s orbital state, we have:
φ1 = φ1* = (1/[πao3]1/2) exp{- r1/ao}
And
φ2 = φ2 * = (1/[πao3]1/2) exp{- r2/ao}
S11 = <φ1|φ1 > = ∫|φ1|2dV = (1/πao3) ∫
exp{- r1/ao}dV
3. Expressionss of the matrix components
The wave functions |φ1> and |φ2> are normalized. Then:
S11 = S22= <φ1|φ1 > = <φ2|φ2 > = 1
S12 = S21 = S = <φ1|φ2 > = <φ2|φ1 >
= exp(- ρ) (ρ2/3 + ρ + 1)
H11 = H22 = E1 + J
J = - ∫φ1*[e2/r2]φ1dV + e2/R
= - (2EI/ρ) [1 - (ρ + 1) exp{- 2ρ}] + e2/R =
- (2EI/ρ) [1 - (ρ + 1) exp{- 2ρ}] + 2 e2/2ρao =
- (2EI/ρ) [1 - (ρ + 1) exp{- 2ρ}] + 2EI/ρ =
(2EI/ρ) [(ρ + 1) exp{- 2ρ}]
H12 = H21 = E1S + K
= - ∫φ1*[e2/r2]φ2dV + e2S12/R
We have :
<φ1|e2/r1|φ2> =
<φ1|e2/r2|φ2> =
2EI (ρ + 1) exp(- ρ)
Then:
K = - 2EI (ρ + 1) exp(- ρ) + e2S/R =
K = - 2EI (ρ + 1) exp(- ρ) + 2EIS/ρ
Overlap integral:
S = exp(- ρ) (ρ2/3 + ρ + 1)
Coulomb integral:
J = (2EI) [(1 + 1/ρ) exp{- 2ρ}]
Resonnance integral;
K = - 2EI [(ρ + 1) exp(- ρ) + S/ρ]
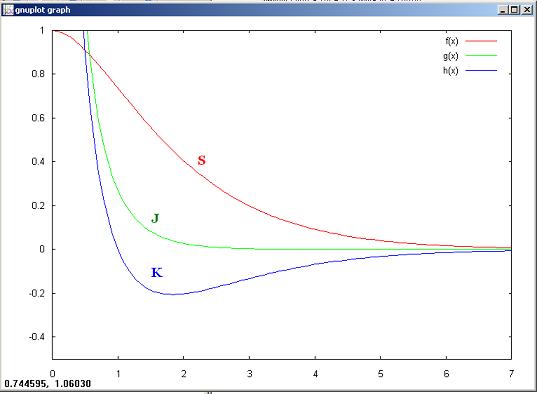
f(x)= S
g(x) = J
h(x) = K
gnuplot> a=1/3
gnuplot> f(x)= exp(- x)*(a*x**2 + x + 1)
gnuplot> g(x) = (1 + 1/x) *exp(- 2*x)
gnuplot> h(x) = -(x + 1) * exp(- x) + f(x)/x
gnuplot> set xrange [0:7]
gnuplot> set yrange [-0.5:1]
gnuplot> plot f(x), g(x), h(x)
|
|