Angular momentum

1. Definitions

1. Moment:

Moment of force (often just moment) = torque
he moment may be thought of as a measure of the tendency of the 
force to cause rotation about an imaginary axis through a point.

2. Momentum:

power residing in a moving object

Momentum is sometimes referred to as linear momentum to 
distinguish it from the related subject of angular momentum.

Like energy and linear momentum, angular momentum in an isolated 
system is conserved.

The angular momentum (L) is defined as the cross product 
of the position vector (r) and the linear momentum vector (p) of 
a paticle of mass m (m) and velocity (v); that is :
p = m v, and L = r x p
In quantum mechanics angular momentum is quantized.

We dfined p as: 
 
P =  - i ℏ∂/∂r

Therefore:
L = - i ℏ r x ∂/∂r

Using Cartesian coordinates, yields:



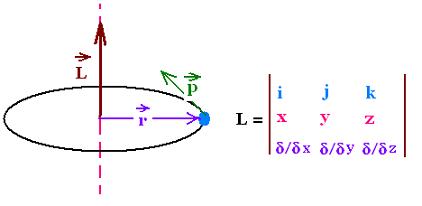We have: 

Lx = - i ℏ(y ∂/∂z - z ∂/∂y)
Ly = - i ℏ(z ∂/∂x - x ∂/∂z)
Lz = - i ℏ(x ∂/∂y  - y ∂/∂x)



2. Commutation relations
Different components of the angular momentum do not 
commute with another while all of 

The components Lx, Ly, and Lz of L commute with 
the square L2 of L. But the components do not 
commute with each other. 


L2 = Lx2 + Ly2 + Lz2 

[L2, Lx] = [L2, Ly] = [L2, Lz] = 0

[Lx, Ly] = iℏLz
[Ly, Lz] = iℏLx
[Lz, Lx] = iℏLy



3. Expression of L2 in spherical coordinates:
Using the related spherical coordinates:

∂/∂x = sin θ cos φ (∂/∂r) + 
cos φcos& theta;/r (∂/∂θ)  - sin φ/ρ (∂/∂φ)

∂/∂y = sin θ sin φ (∂/∂r) + sin φ cosθ/r (∂/∂θ)  + 
cos φ/r sinθ (∂/∂φ)

∂/∂z = cos θ (∂/∂r)  - sinθ/r (∂/∂θ)



We have:

Lx = iℏ [sin φ ∂/∂θ + (cosφ/tanθ) ∂/∂φ]
Ly = iℏ [- cos φ ∂/∂θ + (sinφ/tanθ) ∂/∂φ]
Lz = - iℏ ∂/∂φ


We obtain:

L2 = -ℏ2[(1/sinθ) ∂/∂θ (sin θ ∂/∂θ) + (1/sin2θ) ∂2/∂φ2 ]

That's what we have assumed at the equation (1.7) in:
when we separated the Schrodinger equation, and have written A2 = L2/ℏ2