Quantum Mechanics
Simple harmonic oscillator
Imaginary time

% ---------------------------------------------------
%personal 
%addpath("C:/Octave/Octave-4.0.0/myfiles");
%qsho_code
% © TheScientificSentence.net

%-----------------------------------------------------
%Propagation in imaginary time of the simple harmonic
%oscillator calculation with non dimension parameters
%Gnu Octave or Matlab code .
%
% The related graphs shows the evolution of the wavefunction 
%in imaginary time at different time steps. It converges from 
%a wide gaussian initial arbitrary value to the gaussian ground 
%state.
%----------------------------------------------------------------




% Clearing ------------------------------

clc
clf
clear all


%---------------------------------
kin = 0.067 ; %kinetic energy


% Space  parametres -------------------
Lx=20; %length of x
Nx=10000; %number of x data points
dx=2*Lx/Nx;
x=(-Lx:dx:Lx-2*Lx/Nx);% x-coordinate
kx=pi*[0:Nx/2 -Nx/2+1:-1]/(Lx);% wave vector
k2xm=kx.^2; %wave vector squared


%Time -----------------------------
tf=0.1; %total time
dt=0.001; %time step
NL=tf/dt;% number of time loops


%Potential ---------------------
beta= 5; %beta^2 = mw^2/2
NumAtoms = 10^4;
V= beta^2 * x.^2;

% Other parametres ----------------------
alpha = 100; % mw/h_bar
u=(1/sqrt(pi*alpha))*exp((-.5/alpha)*(x.^2)) ;
u0 = u;


%initializing ---------------------------------
pot=0; E=0; Mu=0; Ur=0; T=0; m=1;


%split opperator method ----------------------
for n=0:NL-1 
v=fft(u); % fourier transform
vna=exp(-0.25*kin*dt.*(k2xm)).*v;
una=ifft(vna);
pot=V ;
unb=exp(-1*dt*pot).*una;
vnb=fft(unb);
v=exp(-0.25*kin*dt.*(k2xm)).*vnb;
u=ifft(v);


% Renormalizing the function --------------
intv=sum(u(:).^2)*dx;
u=(u)./sqrt(intv);
if(mod(n-1,10)==0)
figure(1); clf;
h= plot(x,abs(u).^2);
set(h(1),'LineWidth',2);

xlim([-Lx Lx]) %axes
drawnow;
end

%energy --------------------------------------

dk=dx/(Nx);
Kn=sum( abs(k2xm.*fft(u).^2) )*kin*dk/2; %total kinetic energy
E1=V.*u.^2;
E2=sum(E1)*dx;
E(m)=real(Kn+E2);
E5(m,1)=m;
E5(m,2)=E(m);

end

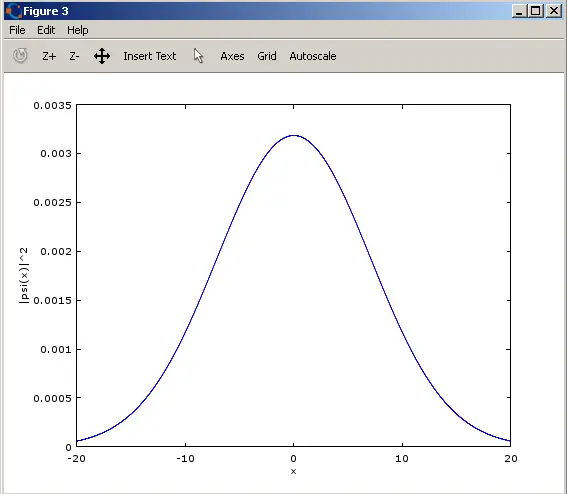
%Ploting of the probability density
figure(3);
plot(x, u0.^2) ;

xlabel('x','Interpreter', 'LaTex')
ylabel('|psi(x)|^2', 'Interpreter', 'LaTex')

 
% ---------------------------------- 


The output at a certain time :