Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Statistical Mechanics
β = 1/κT
Using Classical Mechanics, the average energy for an oscillator is :
< E > = κT
< E > = < (1/2)mv2 > + < (1/2)κx2> =
(1/2)κT + (1/2)κT = κT
< E > = κT
Using Statistical Mechanics, we can write:
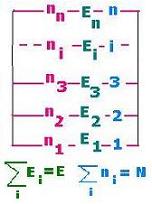
< E > = Σ ni Ei = NΣ Ei exp[- βEi]/Z =
(N/Z)Σ Ei exp[- βEi]= N ΣEi P(Ei)
| |
"i" is the ith level
P(Ei) = exp[-βEi]/ Z
Z = iΣ0 → ∞ exp[-βEi] = 1/β
|
Where: P(Ei) is the probability for ni particles in the
level "i" to have the energy Ei. The sum is related to all the states "i".
The normalization of this probability can be written as:
Σ P(Ei) = 1.
or :
∫ dE P(E)= 1 [from: 0 → ∞]
∫ dE P(E) = (1/Z)∫ dE exp[- βE] =
(1/Z)[- 1/β]exp[- βE](From: 0 → ∞)= β/Z = 1
Thus:
β = 1/Z
We can write:
P(Ei) = β exp[- βE]
We have:
< E > = Σ Ei P(Ei) =
Σ Ei exp[- βEi]/Z =
(1/Z)∫ E exp[- βE]dE
∫ x exp[-β x] dx = (1/β2) ∫ y exp[- y ]dy
Where y = β x
By part;
∫ y exp[- y ]dy; = - y exp [- y] - exp [- y] = - (y + 1)exp[- y]
(form : 0 → n, n is the number of states). We take n large, then:
∫ y exp[- y ]dy = [- (y + 1)exp[- y]] [: 0 → n] = 1
Hence:
∫ x exp[-β x] dx = 1/β2, and
< E > = 1/Z . β2
We have then: < E > = 1/β
And:
< E > = 1/β = κT. Hence:
β = 1/κT
The relationship for the probability becomes:
P(Ei) = (1/κT) exp[- E/κT]
|