Moseley's law

1. Characteristic x rays

When an electron falls from L shell to K shell, the photon (electromagnetic radiation) produced is called the Kα ray. If the process is from M to K , the ray is K_β and son on .. Electrons with lower values of n are more bounded to the nucleus than those with higher values.
The shells correponding to the stationary states are given letter names: the n = 1 shell is called K shell, n = 2, the L shell, and so on.
If enough energy is transferred to a K electron to dislodge it from the atom, the atom will be left with a vacancy in its K shell. The atom is most stable in its ground state, another electron from one of the higher shells will fill the inner-shell vacancy at lower energy emitting electromagentic radiation. We call this an x ray. This x ray carries the energy :
E_K = E₁ - E_{2,3, ...}
This emitted x ray is known also as the characteristic x-ray


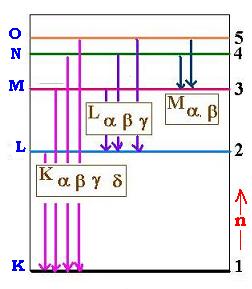
For each element, the energy levels are different, so the characteristic K x-rays are different.

2. Empirical Moseley's law

In 1913, H.G.J. Moseley, working in Rutherford's Manchester laboratory, was engaged in cataloguing the characteristic x-ray spectra of series of elements. He concentrated on the K shell and the L shell x rays produced in an x-rays tube.
By comparing frequencies, Moseley found the following empirical relationship, extracted from his plot Z versus the square root of the meaured frequency:
ν_Kα = (3cR/4)(Z - 1)²
Where : Z is the atomic number , c is the speed of light, and R is the Rydberg constant.

3. Moseley's law from Bohr's atom

Supposing that there are two electrons in the K shell. For an electron L shell, to fill the missing K shell electron, it feels an effective charge (Z - 1) (+ Ze due to the proton and - e due to the remainig K shell electron). Thus the transition between L and K shell (n = 2 → n = 1) involves a photon of wavelength :
1/λ_Kα = R (Z - 1)² [1/1² - 1/2²] = (3R/4)(Z - 1)²
Wich is the same formula found empirically above.