Rayleigh scattering

1. The equation of a moving bound
electron in an electric field

Let us consider an electron bound elastically to its rest position.

When an electric field E is applied on this electron, this latter will undergoes the electric force ( the electric component of the Lorentz force). Let' write this force as: f_e = - e E

This force on the electron displaces it from its first position; the electron then tends to return to it. The related restoring force can be written as:
f_r = - r s
Where s is the displacement of the electron, and r the damping coefficient.
r = m ω₀²
m is the mass of the electron,
ω₀ is the oscillation frequency of the electron.

As a friction in Mechanics, let's assume that the electron undergoes a damping force; wich can be written as:
f_d = d ∂s /∂t
Where d is the damping term = m g ω₀
g is a constant g that is typically much less than unity.

The Second Newton law for the moving electron can be written as:
m ∂²s /∂t² = f_e + f_d + f_r

Then the equation of motion of the electron is expressed as the following differential eqation:
m ∂²s /∂t² = -e E - d ∂s /∂t - r s

This equation takes the form:

∂²s /∂t² + gω₀ ∂s/∂t + ω₀² s = (-e/m) E (1)

2. Rayleigh scattering

Let us now consider the scattering of electromagnetic radiation by such electron described above:

Let's assume that the displacement and the electric field are dependent on time buy the form of : exp(-iωt), then:

s = s₀ exp(-iωt) (2)
E = E₀ exp(-iωt) (3)

The equation (1) takes the form:
- ω² - i gωω₀ + ω₀² = (-e/m) E₀ /s₀ = (-e/m) E/s
Then s = (-e/m) E/ (- ω² - i gωω₀ + ω₀²) (4)
∂²s /∂t² = - ω² s (5)

Substituying (5) in (4), we get:
∂²s /∂t² = - ω² (-e/m) E/ (- ω² - i gωω₀ + ω₀²)

Rearanging, we obtain:
∂²s /∂t² = ω² (e/m) E/ (ω₀² - ω² - igωω₀ ) (6)

Recall that the Thomson cross section is set witout the damping and restoring factors and that it is proportionnal to : <E_out²>/ <E_int²>
and that <E_out²> is proportinnal to <E_int²>
Then the cross section does not depend on <E_int²>

Finaly,
σ_{Total/Rayleigh} = σ_{Total/Thomson} |ω² / (ω₀² - ω² - igωω₀ )|² (7)

After calculating the module between the two||, we find:

σ(Total-Rayleigh)=
σ(Total-Thompson) x ω⁴/[(ω₀²-ω²)²+(gωω₀)²] (8)

When ω = ω₀, we obtain the maximum value of the cross section, that is for resonant scattering. The scattering cross section becomes :
σ_{Total/Rayleigh} = σ_{Total/Thomson} (ω/gω₀)² = (1/g)² (9)

Recall that ω and ω₀ are the frequencies of the incident light and the scattered radiation resectively.

In the case of the binding energy of the electron is greater than the incident energy of the photon ( ω<<ω₀), the relation (8) becomes:
σ_{Total/Rayleigh} = σ_{Total/Thomson} (ω/ω₀)⁴ (9)

In terms of wavelength,λ = c/2πω (9) becomes:

σ_{Total/Rayleigh} = (λ₀/ λ)⁴ (10)

Let's write:
σ(Total-Rayleigh) = constant x 1/λ⁴

Where λ is the wavelength of the incident radiation.

This formula is the scattering cross section of the incident radiation by the medium. It depends on the inverse fourth power of the wavelength of the incident radiation. It is known as the Rayleigh scattering cross section.

The Rayleigh scattering is known as a coherent effect, owing to the fact that no energy is lost acroos the target during the passage of the photon through the target material.

From the formula related to the cross section, the similar relation , related to the intensity can be written as:

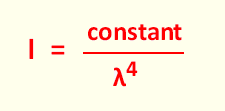
3. The blue color of the sky

These formulas are appropriate to the scattering of visible radiation by gas molecules. In the case of the target medium is the air of the atmosphere, this relationship gives the famous explanation of the blue sky: the air molecules of the atmosphere scatter the shorter wavelength components of the sunlight.



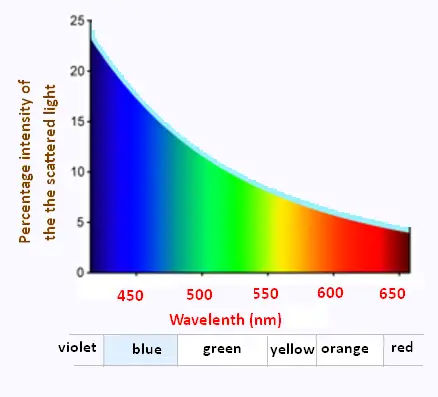
The strong wavelength dependence of the scattering (1/λ⁴) means that shorter (blue) wavelengths are scattered more strongly than longer (red) wavelengths.

4. The white color of the sky

The water droplets in the clouds are many times larger than the wavelength of the incident light, then many shorter in terms of the frequency (ω). In this case σ_{Total/Rayleigh} = σ_{Total/Rutherford}. That is the scattered radiation has the same frequency as the incident light. Foretheremore, the clouds scatter entirely the received light and look white.