Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Statistical theory of the black body thermal rays
1. Introduction
Now that the function u(ν,T) is unknown, we will use the
Statistical Mechanics to find out this function.
Let's consider a cube in the Cartesian space. This cube has
a side "a", then a volume V = a3.
The rays inside the cube form a set of independent
monochromatic radiations.
Each radiation can be represented by a wave of frequency ν.
At a time "t", if the disturbance of the wave is at the
distance "r" from the origin and the wave is propagating in
respect with a certain direction, we can consider the wave
vector k over this direction and write the expression
of wave function of a radiation as:
ψ(r,t) = cos (2πνt - kr)
We know that standing waves are possible inside the cube if
the length of the side "a" of the cavity is a multiple of one-half wavelength of
the radiation. We write this statement as: a = n λ/2
where λ = c/ν and ν is the frequency of the radiation.
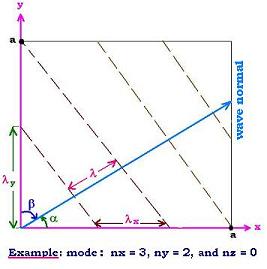
Now, let's consider a wave normal is in some arbitrary direction
(α, β, γ). As shown in the figure, we have:
λ/λx = cos α, λ /λy = cos β, and
similarly λ/λz = cos γ
The conditions of standing waves over the axis x , y and z
are respectively:
nxλx /2 = a , nyλy /2 = a, and nzλz /2 = a
that is:
nxλx /2 = nyλy /2 = nzλz /2 = a
Then:
cosα = λ/λx =λ nx/2a
cosβ = λ/λy = λ ny/2a, and
cosγ = λ/λz/= λ nz/2a.
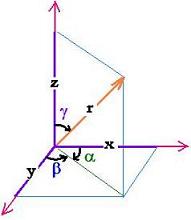
As shown in this figure, for any vector r (x,y,z), we have:
1= (x2 + y2 + z2)/r2. That is:
1= (rcosα2 + rcosβ2 + rcosγ2)/r2
Thus:
cosα2 + cosβ2 + cosγ2 = 1
We have then:
(λ nx/2a )2 + (λ ny/2a )2 + (λ nz/2a )2 = 1
or:
(λ/2a)2[ nx2 + ny2 + nz2] = 1
nx2 + ny2 + nz2 = (2a/λ)2
for the frequencies:
nx2 + ny2 + nz2 = (2a ν/c)2
ν2 = (c/2a)2 [nx2 + ny2 + nz2]
That is the condition to satisfy by a radiation of a
thermal rays, of frequency ν to have stable standing
(stationnary) waves inside the cube.
The number of these radiations make up a continuous
spectrum in the frequency scale.
The all possible radiations in this case could be:
n1 = 0, n2 = 0, n3 = 1 → ν = c/2a
n1 = 1, n2 = 1, n3 = 1 → ν = c/2a 31/2
.....
A triplet (n1,n2,n3) defines completely a standing wave mode
What is the total number of these modes?
2. Number of modes in the cavity of volume V
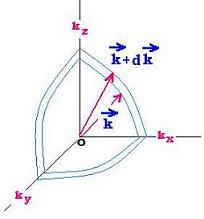
Now we are going to use the wave vectors space k. With a
cubic volume V = a3 equal to a spherical volume V = (4/3)πk3,
we transform the above (nx,ny,nz) condition of normal modes, using k = 2π/λ
and ν = c/λ = ck/2π to:
ν2 = (c/2a)2 [nx2 + ny2 + nz2] =
(ck/2π)2 = (c/2a)2 [nx2 + ny2 + nz2]
Thus:
k2 = (π/a)2 [nx2 + ny2 + nz2]
The wave vector k can thenbe expressed as:
k = (π/a)(nx, ny, nz); that is for any triplet mode
(nx, ny, nz), we have a wave vector that characterizes one radiation
frequency inside the blackbody cavity. (π/a)3 constitutes the elementary
cube, and the k space can be replaced by the n space. The number of
modes defines the number of states for the vector k.
The number of modes "g" inside the positive octant of the space is
the (1/8) times ratio of the volume V = (4/3)πk3 and the elementary
volume (π/a)3; that is:
g = (1/8) (4/3)π k3/(π/a)3 = (1/6π2) k3 a3
= (1/6π2) k3 V = (V/6π2) k3
The number of states in the range k to k + dk is the
derivative of g; that is:
dg = (V/2π2) k2 dk
For the frequencies, using k = 2πν/c then dk = 2π dν/cwe have:
dg = (V/2π2) k2 dk = (2π/c)(V/2π2) (2πν/c )2 dν
dg = 4π V (1/c )3 (ν )2 dν
Thus:
dg = 4πV(1/c)3 ν 2dν
the number of modes inside a blackbody cavity of volume V
related to a frequency ν.
We have two polarization states for one wave. We multiply
by two and divde by the volume of the cavity to obtain the
density of modes inside the cavity:
dg = 8π/c3 ν2 dν
modes' density for a frequency ν.
3. Rayleigh-Jeans Formula
The experiments had given for the spectral energy density u(ν,T)
a distribution analogous to that of Maxwell for the velocities of gas molecules.
Lord Rayleighand Sir James used then for thermal rays the statistical method,
that had worked weel to expalin the thermodynamic properties of body materiels.
The energy equipartition principle that had worked well for gases is then
applied for the thermal rays. Rayleigh and James considered that each radiation mode
(mode of cavity) of frequency ν corresponds to a mode of standing wave of vibration
for a linear oscillator.
This oscillator, having two degrees of freedom, at the equilibrium state, have
to satisfy the the energy equipartition principle: The average energy for
this oscillator is equal to kT, where k is the Boltzmann constant and T is
the temperature at the equilibrium of the cavity in Kelvin degrees.
The energy density ca be then written as:
dU(ν,T) = dg x kT = 8π/c3 ν2 dν x kT
The spectral energy density is du(ν,T) = dU(ν,T)/dν
Thus:
du(ν,T) = dU(ν,T)/dν = 8πkT/c3 ν2
That is the Rayleigh-Jeans formula
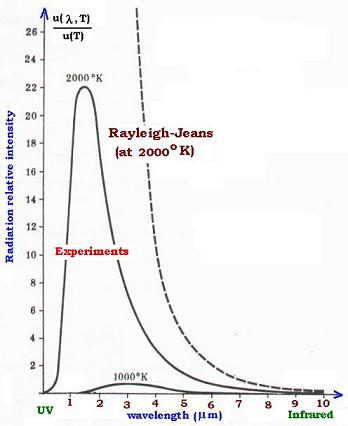 The Rayleigh-Jeans formula represented correctly the experimental
results in the low frequencies region (high wavelengths) such as
the infrared radiations. But the formula was unable to fit the results
in the high frequencies domain (low wavelengths) such as the UV (ultraviolet)
radiations. It leads, however, to an infinite value of the specral energy
density u(ν,T) in respect with the low wavelengths, as we can see in the
equation:
The Rayleigh-Jeans formula represented correctly the experimental
results in the low frequencies region (high wavelengths) such as
the infrared radiations. But the formula was unable to fit the results
in the high frequencies domain (low wavelengths) such as the UV (ultraviolet)
radiations. It leads, however, to an infinite value of the specral energy
density u(ν,T) in respect with the low wavelengths, as we can see in the
equation:
∫ u(ν,T) dν dν [ν: 0 → ∞ ]
= 8π/c3 ∫ν2 = ∞
This divergent integral has no physical sense. At this time, one had
said the Rayleigh-Jeans formula "bursts the ceiling".
The frequency range in the UV region is 0.01 to 0.4 µm. The Rayleigh-Jeans
formula couldn't explain why the energy density drops in this region. It
expected, however, an infinite energy in this UV region. The physicist Ehrenfest
named this circumstance the ultraviolet catastrophe.
Lord Rayleigh and Sir James knew that their formula was incorrect, but
they ignored the way to correct the issue..
|