Attenuation coefficients

1. Expression of the attenuated intensity

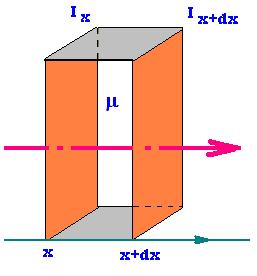
When a narrow beam of mono-energetic photons, such as x-ray, γ rays, penetrates a surface of a material; it experiences a change in its intensity, owing to absorption or scattering that occur during the travel of the beam accross the material. The expression of the intensity of the beam the long of an axis parallel to the direction that photons beam can be calculated as:
dI_x = I_x+dx - I_x = - (I_x - I_x+dx) = - coefficient dx I_x
Or:
dI_x/I_x = - coefficient I_x dx.
Integrated with respect to the thickness of material traversed "dx", and letting coefficient = μ gives:
ln I(x) = - μ x + constant → I(x) = Constant e ^{- μ x}
At x = 0, I(o) = I_o; then, at the traveled distance "x", we have
I(x) = I_o e ^{- μ x}

2. Linear attenuation coefficient

The coefficient μ must have the dimension of length^-1. It is called the linear attenuation coefficient. It is generally expressed in cm^-1.
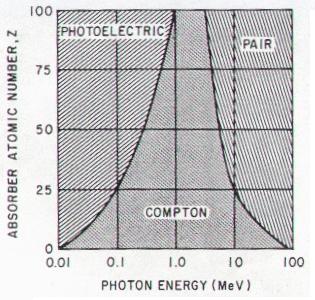
The linear attenuation coefficient μ is defined as the fraction of an incident beam of photons that is absorbed or scattered per unit thickness of the target absorber. The photoelectric effect dominates at low photon energies (< 26 keV) in soft tissue. With higher energy photons at low Z materials, Compton scattering dominates. Rayleigh scattering comprises about 10% of the interactions in mammography and 5% in chest radiography.
The average distance traveled by a photon between two successive interactions is called Mean Free Path (MFP), and can be calculated from linear attenuation coefficient: λ = 1/μ.

3. Mass attenuation coefficient

The coefficient μ is used as μ/ρ and called mass attenuation coefficient, where ρ is the density of the target material. It is usually expressed in units of cm²/g. It is obtained by measuring the values of I_o, I and the thickness "x".

4. Total mass attenuation coefficient

The mass attenuation coefficient is due to absorption coefficient related to the incoherent processes, as the phoelectric effect, Compton effect and pair production; and scattering coefficient due to coherent effect as Rayleigh scattering processes. We write:
μ/ρ (Total) = μ/ρ(absorption) + μ/ρ(scattering), that is:

μ/ρ (Total) = μ/ρ(Photoelectric) + μ/ρ(Pair-Production) + μ/ρ (coherent:Rayleigh) + μ/ρ(incoherent:Compton)

For mixtures and compounds, the values of the mass attenuation coefficients are obtained by additivity: μ/ρ = ∑ w_i (μ/ρ)_i, where w_i is the fraction by weight of the ith atomic constituent.

5. Total related cross section

The cross section that an incident photon makes an effect (absorption or scattering) within the target material is the total cross section due to the attenuation effects; that is the absorption effect and the scattered effect.

σ (Total) = σ(absorption) + σ(scattering), that is:

σ (Total) = σ(Photoelectric) + σ(Pair-Production) + σ(coherent:Rayleigh) + σ(incoherent:Compton)

6. Relationship: μ/ρ and σ

If S is the right area perpendicular to the path of the incident beam of photons through the material, the related volume is V = S dx. Per atom, it is equal to S dx/N, where N is the number of atoms within the volume V. The volume can be expressed as V = m/ρ where m and ρ are respectively the mass and the density of of the volume V of the material. Hence, per atom, we have the surface S_a = V/dx = m_a/ρdx. Per unit length, the surface S_a is called the cross section that the incident photon makes an effect with the target atom and denoted σ. Therfore dx = 1/μ.We have then ρ = m_aμ/σ. With m_a = u A/N_a (u is the atomic mass unit, A is the relative atomic mass of the target element, and N_a the Avogadro number), the product μ/ρ takes then the following form: μ/ρ = σ N_a/uA.

μ/ρ = σN_a/uA [per atom and per unit of thickness]

Where:
σ is the cross section per electron (the probability that the incident photon makes an effect in the target element),
ρ the density of the material target,
N_a is the Avogadro number (6.023 ²³/mol),
u is the atomic mass unit (mass of an atom of nuclide ¹²C/12), and
A is the relative atomic mass of the target element.

7. Mass energy transfer coefficient

The mass energy transfer coefficient is the product of the mass attenuation coefficient and the fraction of energy transferred to the charged particles as kinetic energy, by the interacting incident photons. That is the fraction "ƒ" of the mass attenuation coefficient that produces kinetic energy forejected electrons from their atomic shell.
It is written as: μ_tr/ρ. We have:

μ_tr/ρ = N_a/uA x {ƒ_phσ(Photoelectric) + ƒ_ppσ(Pair-Production) + ƒ_cohσ(coherent)}

where the low contribution of the σ(incoherent:Compton) transfert is neglected. ƒ_x is the related process fraction.

For mixtures and compounds, the values of the energy transfert coefficients are obtained by additivity: μ_tr/ρ = ∑ w_i (μ_tr/ρ)_i , where w_i is the weight of the ith atomic constituent.

8. Example of the mass attenuation coefficients graph
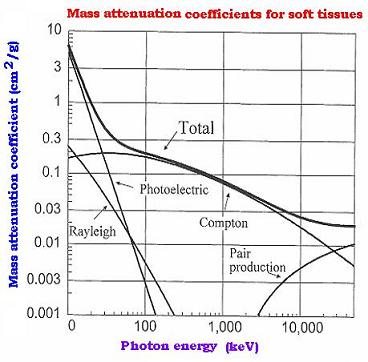