Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Black body's radiation
1. Abstract
A heated object emits radiation. The intensity of this radiation depends on the material itself and the temperature at which it is heated.
This emitted radiation is an electromagntic radiation. It propagates at a straight line in vacuum, with a velocity equal to the speed of light c . It can be decomposed by a spectrometer to produce a series of constituent monochromatic radiations. Each one is caracterized by a periodic phenomenun of frequency ν and wavelength λ = c/ν. A monochromatic radiation is represented by a transversal wave travelling in the direction of its wave vector k of magnitude 2π/λ. Electromagnetic radiations can stem from other sources as electric discharges All the electromagnitic radiations have something in common, they carry energy. In this document, we will focus only on the thermal radiation which is radiated from a calorific energy of a source.
2. The radiated energy
The total emission of a source is measured by its radiated power, that is the quatity of energy W emitted by unit time across its surrounding. The energy dW of the radiations that correspond to the range of wavelengths between λ and Λ + dλis expressed by:
dW = W(λ)d&lambda:, where W(λ)is the energy of the wavelength λ emitted by the source, so that: W = ∫ dW = ∫ W(λ)dλ [0 → ∞] because the total emission contains all of the possible wavelenghts].
3. The energetic luminance of the emission source
As in Optics, radiation propagating in a straigt line in a homogeneous and isotropic environment are formed by rays and beams. Let's consider the following figure:
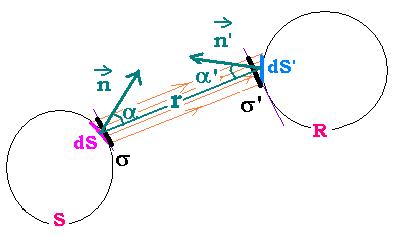
Th source S emits radiation that is meseared by the receptor R. dS, little portion of the source S, has a normal vector n and which makes an angle α with the direction SR. n' is the normal vector to the face of the receptor. To make dS and dS' parallel, we replace them respectively by dσ and dσ', where dσ = dS cos α and dσ' = dS' cos α'. We assume that dS and dS' are little relating to the distance r between the source and the receptor; so that all the rays from the source have the same direction as r and the solid angle dΩ of the cone formed by the rays from a point in dS has the same value dΩ = dσ'/r2 for all the points of the surface dS.
The energy dW emitted by dS, carried by the beam, and reached by dS' is proportional to dσ and dΩ. We cab write:
dW = e dσ dΩ
the coefficient e depends on the nature and the temperature of the source, as well as the wavelength of the emitted radiation. It is called energetic luminance of the source in the direction r. For the receptor, It depends also on the direction of radiation emission(α.
If the beam carries only the radiation energies related to the range of wavelengths λ and λ + dλ, we can write:
dW(λ) = dW dλ = e(λ) dσ dΩ, so that e = ∫ e(λ)dλ and W = ∫ W(λ)dλ [λ: 0 → 0 ∞]
e(λ) is called monochromatic energetic luminance of the source dS in the direction R for the wavelength λ
From the relationships: dS = dσ cos α dS' = dσ' cos &alpha'; dΩ = dS'/r2, and dW = e dσ dΩ, we find:
dW = e dS cos α dS' cos α'/r2
Which is the Lambert's formula
Remark:
 For several numbers of the sources, the coefficient e do not depend on the direction of the emission.
We say that the source emits according to the Lambert's law. From whatever place, the receptor receives
the same total energy from all the sources.
For several numbers of the sources, the coefficient e do not depend on the direction of the emission.
We say that the source emits according to the Lambert's law. From whatever place, the receptor receives
the same total energy from all the sources.
4. Absorption factor
The energy emitted by a source regarding the range of wavelengths λ and λ + dλ and received by a body is reflected, or transmitted, or scattered. The important part is absorbed by the body receptor. If W(λ) is the radiated energy and W'(λ) the obsorbed, the rate a(λ) = W'(λ)/W(λ) is called spectral absorption factor. The quantity a = ∫ a(λ) dλ is the absorption factor.
In the particular case where all the radiations are reflected or scattered, we say that the body is perfectly absorbing or perfectly scattering. When a body absorbes all the radiations,that is the value of its absorption factor is 1; and as it reflects no radiation, it appears perfectly black, we say that the body is a black body. All the radiations absorbed by a black body are transformed into heat.
5. How to realize a black body?
Here is the technique used by the physisicist Wien. It consists on a box solid, closed, empty and impermeable to the rays that can come from its outside; and presenting a little openinig which the interior surface is covered by an absorbing substance such as a soot.
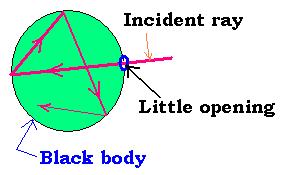 An incident ray goes through the box across the little opening, after some reflexions, this ray disappear because it's totaly absorbed.
An incident ray goes through the box across the little opening, after some reflexions, this ray disappear because it's totaly absorbed.
In the reverse, if the body is heated to a certain temperature T, the body will emit a radiation from the inside wall of the box and will propagate continuously. The radiation that exits across the little openinig is called the black radiation, that is the radiation of the black body at the temperature T.
6. Thermal equilibrium in the black body
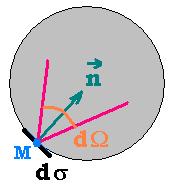
In a black body box, closed, isothermal, and maitained at the temperature T, the inside wall emits,
receives and absorbes radiations. After a certain time, all the parts of the box are at the same
temperature, a stationary satte is established. We say that the radiations are in the thermal equilibriun
inside the black body.
From the point M on the surface dσ, inside the box, the radiation beam carries an energy
equal to dW (λ)= E(λ) dσ dΩ dλ for the range λ and λ + dλ.
E(λ) is the spectral luminance. E = ∫ E(λ)dλ, dW = ∫ dW(λ) dλ = E dσ dΩ.
The luminance E do not depend on theemission direction.
7. Kirchhoff Law
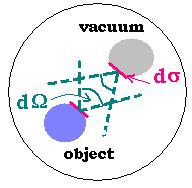 Let's put a body with a monochromatic energetic luminance e(λ) and a spectral absorption factor a (λ)
in a box maintained at the temperature T. At the temperature equilibrium, the temperature of the body and the box
are the same. The body will emits the amount of energy that it receives. The beam of radiations, in the range λ
and λ + dλ, characterized by dσ and dΩ that it emits, carries the energy
dW(λ)= e(λ)dσ dΩ dλ
Let's put a body with a monochromatic energetic luminance e(λ) and a spectral absorption factor a (λ)
in a box maintained at the temperature T. At the temperature equilibrium, the temperature of the body and the box
are the same. The body will emits the amount of energy that it receives. The beam of radiations, in the range λ
and λ + dλ, characterized by dσ and dΩ that it emits, carries the energy
dW(λ)= e(λ)dσ dΩ dλ
If we take a space portion inside vacuum of the box; and consider the same dσ and dΩ, this portion will
radiate the energy dW0(λ)= E0(λ)dσ dΩ dλ
E0(λ) is called specific spectral intensity of the thermal radiation in the vacuum of the box.
It the amout of energy dW0(λ) emitted by the vacuum portion is absorbed in part by the body inside the
box, it will emit the amount a(λ)dW0(λ). Hence, we can write a(λ)dW0(λ) = dW(λ) or
a(λ)E0(λ)dσ dΩ dλ = e(λ)dσ dΩ dλ and find the Kirchhoff law:
e(λ) = a(λ)E0(λ)
Remarks:
1. If the body inside the box is a part of the wall of the black body itself, we can write:
E(λ) = E0(λ) since the a(λ)≡ 1 and e(λ)≡ E(λ)
for the blackbody. We can say then that, for the black body, the spectral luminance is equal to its specific
spectral intensity at a given temperature.
2. The experiments show that E(λ) do not depends on the nature of the wall of the box. The main dependance
are on the wavelength and the temparature. E(λ, T) is a universal function of the temperature and the wavelength
E(λ, T) is called specific spectral intensity of the black body.
We ca write E(T) = ∫ E(λ, T)dλ called total spesific intensity of the black body.
8. Emissive power of the black body
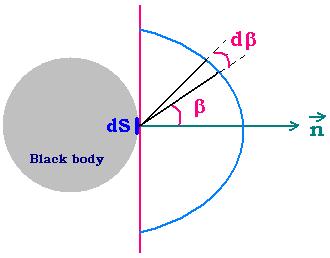
At a certain temperature, the total spesific intensity E(T) of the black body is the same in each
point of the black body.
The radiation coming from the opening dS to the point M can be written as:
dW = E dσ dΩ = E dS cos β dΩ where dσ = dS cos β.
The total power P radiated by dS over all the space is calculated as follows:
dP = dW/dt = E (dS/dt)cos β dΩ = 2π E (dS/dt)cos β sin β dβ, hence:
P = 2π ∫ E (dS/dt)cos β sin β dβ = 2π E (dS/dt) ∫ cos β sin β dβ .
∫ cos β sin β dβ = ∫ sin β d(sin β)
= (1/2)sin2 β [0 → π/2] = 1/2.
Hence:
P = 2π E (dS/dt) (1/2) = π E (dS/dt)
For a unit area and unit time; at the temperature T:
P(T) = π E(T)
9. Energy density of the thermal radiation
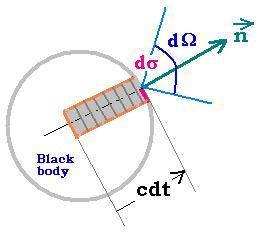 Radiations propagate at the speed of light c. If for a given time dt, dW = E dS cos β dΩ is the
energy leaving the black body accross dS, this amount will be equal to the marked part inside the black body;
that is dW = c dt dσ dU , where dU is the energy per unit volume. We have:
Radiations propagate at the speed of light c. If for a given time dt, dW = E dS cos β dΩ is the
energy leaving the black body accross dS, this amount will be equal to the marked part inside the black body;
that is dW = c dt dσ dU , where dU is the energy per unit volume. We have:
c dt dσ dU = E dσ dΩ, or
For a unit time,
dU = E dΩ/ c → U = (1/c) ∫E dΩ = (4π/c) E
Let's write:
The energy spectral density of the black body:
U (T, λ)= (4π/c) E(T, λ),
and
The total energy density of the black body:
U (T)= (4π/c) E(T)
10. Pressure of radiation
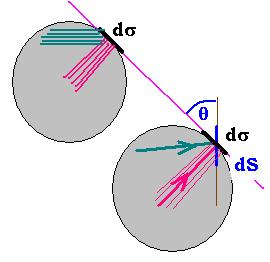
The pressure exerted on the element of surface dS by (dF) the radiation inside the black body is dP = dF/dS = dF cos θ/dσ = dF cos θ/dσ.
We can write: dW = dF c dt, then dP = (dW/c dt) (cos θ/dσ)= dW cos θ/dV = dU cos θ, where dV = dσ c dt the volume unit.
the pressure exerted normally to dS is: dP = dU cos2 θ.
We have seen that the energy density is dU = E(T)dΩ/c;. We can then write:
dP = dU cos2 θ = (E(T)dΩ/c)cos2 θ
Integrating, we obtain: P = (2 πE(T)/c) ∫ cos2θ sin θ dθ = (2 πE(T)/c) (- 1/3) cos3θ [0 → π]= (2 πE(T)/c) (2/3) = (4 πE(T)/c) (1/3).
We have: U(T) = 4 πE(T)/c ; then:
P = U(T)/3
The pressure exerted by the radiation on the wall of the black body is equal to the third of the total energy density of this radiation.
|