Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Structure of the atom
Bohr atom
1. Classical model of the atom
After the work of Rutherford on 1911, it is stated that the atom is composed of a
nucleus and electrons moving around. In this study, It is considered the simplest atom, hydrogen.
The force between the electron and the proton (nucleus) is given by the Coulom's law:
Fe = - (1/4πε0)(e2/r2) er (1.1)
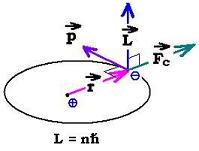 Where:
Where:
. Fe is the Coulombian electrostatic force exerted by the proton on the electron.
. - e is the charge of the electron (+ e is the charge of the proton),
. r is the distance between the two particles, and
. er is the unit vector in the direction from the proton to the electron.
This Fe needs to be balanced by the centripetal force Fc in order to maitain
the electron of mass m moving (rotating) at constant tangential speed v in a circular
orbit of radius r.
This phrase is written as: Fe = Fc, that is :
(1/4πε0)(e2/r2) = m v2/r (1.2)
We have then:
v = e/[4πε0mr]1/2 (1.3)
The kinetic energy of the system is the kinetic energy of the electron because
the proton is so massive regarding the electron (mp ≈ 1836 mee).
We can then consider that the proton is at rest. Then KE = (1/2)mv2 .
The Coulomb potential of the electron (Origin at the proton) is PE = - e2/(4πε0 r)
Using the equation (1.2), we obtain: PE = - mv2 = - 2 KE
The total energy of the atom is E = KE + PE = KE - 2 KE = - KE = PE/2
Total Energy E = - e2/(8πε0 r) (1.4)
In this expression, energy is negative, just to show that it cannot given by
the system (atom); instead it must be received in order to move the electron.
That is the electron is bounded. When r decreases, - E incereases, so
E decreases.
2. Bohr atom
Bohr's general assumptions (Postulates) in order to derive the Rydberg equation.
1. It exists for the orbiting electrons in atoms some stationary states
in which they do not radiate electromagnetic energy.
2. The emission or absorption of electromagnetic radiation for an atom occurs
only relatively to the transition of electrons between two stationary states. The
frequency ν of the related (absorbed or emitted) radiation obeys the equation:
ΔE = (h/2π) ν. ΔE is the energy difference between two stationary states and
h is the Planck's constant.
3. The classical laws of Physics govern the dynamical equilibrium of the system in
the stationary states, but they are not applicable to transitions between states.
4. For circular motion, the angular momentum of the system (electron-nucleus) in a
stationary state is an integral multiple of (h/2π).
For circular motion, the angular momentum L of the electron is: L = r x p. Its
magnitude is L = mvr. This angular momentum should be (Assumption 4) as follows:
mvr = n (h/2π), or:
n is called the principal quantum number. It quantizes all the related physical
values such as velocities, radii and enrgies.
v = nh / 2πmr (2.1)
Equating (1.3) and (2.1), we get:
rn = (4πε0)n2(h/2π)2 /m e2 (2.2)
Only certain values of the radius r are allowed.
The equation (2.2) can be written as:
rn = n2 a0, where a0 is called the Bohr radius:
Where:
a0 = r1 = (4πε0)(h/2π)2 /m e2 (2.3)
a0= 0.53 x 10 - 10 m
1/4πε0 = 8.99 x 10 9 N.m2/C2
h/2π = 1.055 x 10 -34 J.s
m = 9.11 x 10 -31 kg
e = 1.6 x 10 -19 C
The value n = 1 gives r1 = a0, the radius of the hydrogen atom in its lowest
energy state, called the ground state. The other values for which n> 1, correspond to the
excited states of the atom.
The diameter of the atom is about 2a0 ≈ 10 -10 m; that is 1 Angstrom (Å).
The total energy in the relationship (1.4) is written: En = - e2/(8πε0 rn). Also
only some values of energy are pemitted. En is the energy of an electron in the stationary state n.
Using the equation (2.2), we get:
En = - e2/(8πε0) [1/a0 n2] = - E0/n2 (2.4)
Where E0 is the lowest energy state:
- E0 = E1, the lowest energy ( state n = 1).
E0 = e2/(8πε0) (m e2/(4πε0)(h/2π)2) = [m e4/2(h/2π)2][1/4πε0]2 = 13.6 eV (2.5)
En = - E0/n2 (2.6)
E0 = [m e4/2(h/2π)2][1/4πε0]2 = 13.6 eV (2.7)
The atom can then exist only in the stationary states with definite and quantized energies En.
When an electron undergoes a transition from En to Em, the radiation emitted
(or absorbed) of frequency ν and wavelength λ occurs the following way:
En - Em = h ν
Using the equation (2.6) and ν = c/λ yield:
c/λ = (1/h)(- E0/n2 + E0/m2) = (E0/h)(1/m2 - 1/n2)
Then:
1/λ = (E0/hc)(1/m2 - 1/n2)= R∞(1/m2 - 1/n2) (2.8)
Where :
R∞ = E0/hc (2.9)
R∞ = 1.097 x 107 m- 1 is called the Rydberg Constant. The subscript
∞ stands for the infinite nuclear mass, regarding the mass of the orbiting electron. This value agrees
with the experimental value of Rydberg.
The emitted radiation is called is called a photon or a light quatum.
Using the equation (2.1), we get the speed of the electron moving around its nucleus:
vn =nh/2πmrn=nh /2πma0n2 = h/2πmna0 (2.10)
v1 = h / 2πm a0 = 2.2 x 106 m/s
The ratio:
α = v1/c ≈ 1/137 is called the fine structure constant.
3. The Bohr's Correspondence Principle:
It states:
In the limits where classical and quantum theories should agree,
the quantum theory must reduce to the classical result.
Example:
Classical electodynamics gives the frequency of the electron in its
orbit around the nucleus:
νClassical = 1/T = ω/2π = (1/2π) v/r (3.1)
Using the new quantized values of rn and vn (2.2) and (2.10), we find:
v/r = (h/2π)(1/n3 m a02). the equation (3.1) becomes:
νClassical = [h/1/(2π)2][1/n3 m a02] (3.2)
The Bohr's model gives the frequency νBohr of the transition from the state
n + 1 to the nearest state n. The equation (2.9) yields:
νBohr = [E0/h][(1/n2) - (1/(n + 1)2)] = [E0/h][(2n + 1)/n2)(n + 1)2]. (3.3)
The approximation for large orbits, that is for large values of
the quatum number n, we have:
νBohr = 2E0/hn3. The two frequencies are equal and the Bohr's
correspondance is verified.
4. An improvement of the Bohr atom
4.1. Reduced mass correction
In fact, the mass of the nucleus is not infinite. the system (nucleus, electron)
rotate about the center of mass. The mass in the previous equations would be
the reduced mass μ of the system.
The more accurate Rydberg constant becomes then , for the hydrogen atom:
RH= R∞ μ/m = R∞ / (1 + m/M) (5.1)
We have RH = 1.096776 x 107 m- 1, which fits the measuremements.
4.2. Model for the hydrogeneic
The Bohr model may be applied to the hydrogen-like, that is the sigle-electron atom
such as H+, Li++. Because of he Coulomb interaction (between Ze and e), the e2 in Bohr's formulas
becomes Ze2, where Z is the Atomic number of the atom. The
Rydberg constant R changes into Z2R and the Rydberg equation becomes:
1/λ = Z2R[(1/ni2) - (1/nf2)] (5.2)
5. Frank & Hertz Experiment
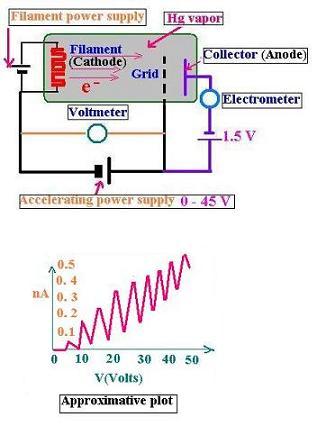
The German physicits James Franck and Gustav Hertz (nephew of Heinrich Hetz),
in 1914, wanted to study the ionization phenomenun. They used an electron
bombardment of gaseous vapors. The above figure describes the experiment.
Electrons extracted from a heated filament (cathode) are accelerated by a
varying voltage (0 - 45 V)controlled by a voltmeter. these electrons
ionize the monoatomic gas Hg.
The extracted electrons arrive at the grid and then decelerated between the grid
and the electrometer (sensitive ammeter). As the potential difference between the
electrometer is only 1.5 V, that means only the electrons with energy equal to
1.5 eV can be detected by the electrometer device. The extracted electrons with
energy less than 1.5 eV do not pass; the electrons with energy more than 1,5 eV are
decelerated and then detected.. The results are as follows:
If the accelerating power supplies is less than 5 V (then the energy of the
electrons are 5 eV), a current is detected (all the elctrons within the energy range
1.5 to about 5 eV). The electrons do not lose energy, the collisions are elastic.
When the voltage is icreased to about 5 V (precisely 4.88 eV), the current drops
suddenly. The collisions becomes inelastic. That is, all the electrons with 4.88 eV
do not go to the grid, they excite the gas atoms. The same process occurs with
electrons at energy about 10 eV (precisely about 4.88 x 2 = 9.76 eV). The expected
ionization process (wich would occur with very high energy)turns out to be excitation.
The electromagnetic radiation (photon) were not seen because they are not in the visible
spectra. Nevertheless, an emission line of wavelength 254 nm (Ultraviolet) was measured.
Setting E = 4.88 eV, and used the Planck relationship E = hν Franck and Hertz showed
that the Planck constant was in good agreement with the values determined by others. This
experiment is another explanation way to verify the quatization of energy.
It exists other highly states in Hg that could be excited ( from
L to M , N to L , ...) in enalstic collisions; but the probabilty of that
occurrence is more smaller that the first (from L to K , M to K , N to K)
excited states.
6. Hydrogen Spectra: related formula
6.1. Balmer's formula
Johann Jakob Balmer, a Swiss mathematician and an honorary physicist, in 1885,
heated a Hydrogen tube and analyzed the lines emitted. He established an
empirical formula for the spectral lines of the Hydrogen atom and obtained:
λ = hn2/(n2 - 22)
This relationship gives the value of the wavelength emitted by the hydrogen
atom.
h is a constatnt equal to 3.65 x 10- 7m
n = 3, 4, 5, 6, and so forth.
| n | 3 | 4 | 5 | 6 | 7 |
| λ(nm) | 656 | 486 | 434 | 410 | 379 |
| color | red | green | blue | indigo | violet |
v
6.2. Rydberg Formula
In 1888, Johannes Robert Rydberg, Swedish physicistinverted both sides of
Balmer's formula and gave:
1/λ = RH[(1/22) - (1/n2)]
RH is the Rydberg constant = 0.010972 (nm)- 1
7. Comments:
7.1. Why the postulate #1?
Due its circular motion about the nucleus, the electron is accelerated. An
accelerating charged particle looses (gives off or radiates)energy in the form
of electromagnetic radiation ( as light, xray, ...). If energy of the electron
decreases continusly, then its radius deccreases continusly, spiralling inward
until it crashes into the nucleus, so the atome collapses!
7.2. Bohr Model
Bohr strived to build an ad hoc theory to account for the
hydrogen spectral lines experimented by Balmer. He said himself: " As soon as I saw the
Rydberg formula, everything became clear to me". The set hypothesis mvr = nh/2π,
matched the predictions and became then the found key formula; that is the angular
momentum is quantized. The quatization of energy was already thought before by Max Planck. The introduction
of the integral number n gives the discrete values for the related values such as radius, velocities and
energies. This hidden quantization feature appears in the experimental (empirical) Rydberg formula.
Whilst the Bohr model was a major step toward understanding the quantum theory of the atom,
considering a circular orbiting motion of the electron (as a planet) around the nucleus is just
approximative; setting definite values for the radius and momentum violates the uncertainty principle in
which position and momentum cannot be determined simultaneously.
The correct motion of the electron and the explanation of the brightness of the spectral lines
will be described by the probability of presence (charge distribution) and the transition
probabilities (spectra) concepts derived from Quantum Mechanics.
|