Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Statistical Mechanics
Maxwell-Boltzmann distribution
1.Introduction
In the real microscopic world, it does not exist a particle alone inside any space. Dirac
relativistic equation or Schrodinger's equation inform us about the single electron behavior in an atom.
But when it come to try to do so with many electrons, the issue turns out to be very complicated.
Kinetic theory of gases tells us that the internal energy of a gas is
function of the temperature (more precisely U = (3/2) NkT, derived from the calculation of the mean
square of the particle's speed) and involves only macroscopic terms. But what about the energy
of each particle in the gas?. The only convenient way is to take the system as a whole,
as an ensemble and studying in-depth this system statistically whereby to understand the
structure of this matter by knowing how the energy is distributed among the particles. That is the
purpose of the Statistical Mechanics
What do then "microscopic" and "macroscopic" stand for?
When one specifies in depth all the parameters of a particle of a system, we have
a microstate for this system. Whereas, when a "global" situation
of a system is considered, a kind of "snapshot" of the situation, we have
a macrostate for this system.
2. Macrostates & Microstates
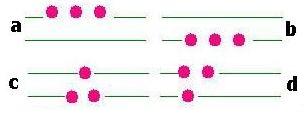
Let's consider the following example:
We have 3 particles and 2 energy levels. If the particles are indistinguishable,
we have then 4 configurations.
If the particles are distinguishable, we have 8 configurations.
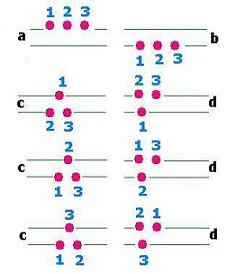
The number of macrostates is 4
4: Ω(a), Ω(b),Ω(c),Ω(d).
The number of microstates is 8
1 for Ω(a) and for Ω(b), and 3 for Ω(c) and Ω(d).
Remark
In the case of indistinguishable particles, every macrostate has no microstate. Forethermore:
Ω(a) = Ω(b) = Ω(c) = Ω(d) = 1. In other words, the macrostate is the
microstate.
Now, let's fix the energy of this system with three particles to be E. Particles can occupy
the two energy levels ni (i = 1, 2).
If Ei (i = 1, 2) is the value of the energy associated to the level i, then:
E = Σ ni Ei [i = 1, 2].
As the total number of particles is already fixed to be N (here N = 3), if the number of
levels is n; we have:
E = Σ niEi
N = Σ ni
[i: 1 → n]
Now, having ni particles in each livel "i", that determines the macrostate for
the system, how many microstates do we have for this macrostate?
If n1 is the number of particles that lodge in the level "1", the number of ways
to have this occupation is the number of combinations for n1 particles
among N particles; that is :
C1 = C(n1, N) = N!/n1!(N - n1)!
Once this case is set; it remains (N - ni) particles to consider.
If n2 is the number of particles that lodge in the level "2", the number of ways
to have this occupation is the number of combinations for n2 particles
among (N - n1) particles; that is:
C2 = C(n2, (N - n1)) = (N - n1)!/n2!((N - n1) - n2!
...
Finally, if the last level contains nn particles = N - n1 - n2 - ... - nn - 1, then
the numbers of ways to distribute them in the last level "n" is Cn = C(nn, nn) = 1.
In total, the number of ways we have is the product of all the combinations. That is:
C1 x C2 x ... x Cn = ΠCi [i: 1 → n]
= N!/n1!(N - n1)! x (N - n1)!/n2!((N - n1 - n2)! x ... x 1.
= N!/n1 x n2 x ... x 0!= N!/Πni [i: 1 → n]
The number of ways to distribute N particles over
n levels containing each ni particles is:
Ω = N!/Πni! [i: 1 → n]
This result is related to one configuration. The number ni can take any vlaue
from 1 to n. In total, we have
&sum Ω [i: 1 → n] = (N + n -1)!/N!(n-1)!
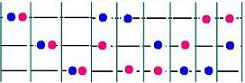 In the example at left, we have 32 = 9 ways to place two distinguishable
particles in three sub_levels.
In the example at left, we have 32 = 9 ways to place two distinguishable
particles in three sub_levels.
In the case of a level "i" has a degeneracy gi; that is the number gi
subshells, we can place ni particles within by gini ways; Thus:
The number of ways to distribute N distinguishable particles over
n levels containing each ni particles; with a degeneracy gi for
the level "i" is
Ω = N! Π(gini/ni!) [i: 1 → n]]
The configuration (n1, n2, ..., ni, ..., nn) represents a macrostate
which has Ω = N! Π(gini/ni!) microstates
3. Maxwell-Boltzmann distribution
Let's suppose that we toss up two dimes. The outcomes can be:
(heads, heads); (tails, tails); (heads, tails) or (tails, heads) because we distinguish the pieces. The probability for
each case is 1/4. If instead we have four balls, red and yellow, then indistinguishable, we will have the case: (red, red);
(yellow, yellow); (red, yellow) = (yelow, red). The probability for each case is 1/4, 1/4, 2/4. We say that the last
case is most probable.
We are interested in the most probable case. To find the most probable case from the expression of Ω we derive
it with respect to the number of particles ni and zero it in order to find the extrema which give the most
probable configuration.
From the expression of Ω itself, we can not go further. Taking its Neperian logarithm "ln" will simplify
greatly the issues.
Ω = N!Π (gini/ni!), thus:
ln (Ω)= ln N! + Σ [niln gi - ln ni!]
Using the Stirling's approximation
ln x! = x ln x - x , we have:
ln (Ω) = N ln N - N + Σ [niln gi - ni ln ni + ni] =
N ln N + Σ [ni][ln gi - ln ni] =
N ln N + Σ [ni][ln (gi/ni)]
Thus:
d[ln (Ω)]/dni = ln(gi/ni) - 1 = ln gi - ln ni - 1
Stirling's approximation proof:
ln N! = Σ ln x [x: 1 → N] = ∫ ln x dx [x: 1 → N]
= xln x - x [x: 1 → N] = Nln N - N + 1.
Neglecting 1, because N is large, we can write: ln N! = Nln N - N.
Example: For N = 100, we have ln N! = 364 and Nln N - N = 360; an error ≈ 1% !
We have the following constraints:
N = Σ ni
E = Σ niEi
Or :
N - Σ ni = 0
E - Σ niEi = 0
If ∂ln(Ω)/∂ni = 0, a linear combination with the
constraints gives also zero (method using constants called Lagrange multipliers).
Let's define then a new function F as follows:
F(ni) = ln(Ω) - λ(N - Σ ni) + β(E - Σ niEi)
= NlnN + Σ [ni][ln (gi] - Σniln ni - λ(N - Σ ni) + β(E - Σ niEi)
To find its extrema, Its zero-derivative gives :
∂F(ni)/∂ni = 0
That is:
ln gi - ln ni - 1 + λ - β Ei = 0
Let's set: λ - 1 = α; then:
ln (gi/ni) + α - β Ei = 0 .
Or: ln (gi/ni) = - α + β Ei
Or: ln (ni/gi) = α - β Ei
Thus:
ni = gi exp[ α - β Ei];
and
N = Σ ni = Σ gi exp[ α - β Ei]
= exp[ α] Σ gi exp[ - β Ei], that gives:
exp[ α] = N/Σ gi exp[ - β Ei] = N/Z
Where:
Z = Σ gi exp[- β Ei] called the partition function. It follows that:
Maxwell-Boltzmann distribution:
ni = gi N exp(-βEi)/Σ gi exp(-βEi)
= gi N exp(- βEi)/Z
without degeneracy: gi = 1, we have:
ni = N exp(-βEi)/Σ exp(-βEi)
= N exp(- βEi)/Z
|