Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
The Compton Effect
1. Abstract
The photoelectric effect used the fact that
energy is conserved with a collision between a
photon and an electron at rest in a metal.
the involved energy of the incident photon is on the same
order of magnitude as the binding energy of an
electron to a nucleus , that is few eV.
However, if the energy of the photon is large
compared to the binding energy of the electron, that is
several KeV, therefore, both conservation of momentum
and energy could be considered.
Compton used this fact in an experiment of
scattered x-ray radiation off of a
graphite block to measure the inrease of the
wavelength of the x-rays.
2. Introduction
The Compton effect, known as incoherent effect was observed by Arthur Compton in 1923.
This Compton Scattering is about an interaction between an
incident gamma photon and an electron at rest.
The incident particle-wave loses enough energy to an
orbital electron to cause its ejection, that is to ionize the
related atom.
After the collision, the incident photon becomes lower in energy, then
infrequency, and then large in wavelength with an emission direction different
from that of before the collision.
Compton scattering is considered to be the principal absorption mechanism
for gamma rays in the intermediate energy range 100 keV to 10 MeV.
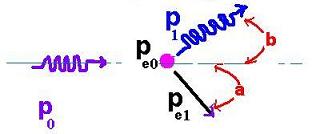
- P0 Incident photon's momentum,
- Pe0 Stationary electron's momentum,
- P1 Scattered photon's momentum,
- Pe1 Recoil electron's momentum,
- a , b Scattering and recoil
angles respectively.
3. Compton wavelength
The conservation of momentum is written as:
P0
+
0
=
P1
+
Pe1
Solving for Pe1, we have:
Pe12
=(
P0
-
P1)
2
=
P02
+
P12
-2
P0P1
=
P02
+
P12
-2
P0P1cos (b)
We know that:
P0
=
hv0/c
P1
=
hv1/c
Then:
Pe12
=
(hv0/c)2
+
(hv1/c)2
-2
(hv0/c)( hv1/c) cos (b)
(Eq.1)
The conservation of energy is written as:
E0+ Ee0=E1+Ee1
We know that :
E0=hv0and
Ee0=mec2and
E1=hv1 and
Ee1=sqrt (pe12c2+me2c4)
Solving for pe12, we have:
pe12c2= Ee12
-
me2c4
Using :
Ee1= E0+ Ee0-E1
we get:
pe12c2
=
(hv0+mec2-hv1)2
-
me2c4
(Eq.2)
Equating (Eq.1) and (Eq.2), we have:
(hv0)2
+
(hv1)2
-2
(hv0)( hv1) cos (b)
=
(hv0)2+ (hv1)2
-
2hv0hv1
+
2 (hv0 -hv1) m ec2
(hv0)( v1) cos (b)
=
hv0 v1
-
(v0 -v1) m ec2
hv0 v1(1-cos (b))
=
(v0 -v1) m ec2
hc/w0 c/w1(1-cos (b))
=
(c/w0 -c/w1) m ec2
hc (1-cos (b)
=
(w1 - w0) m ec2
Where w =c/v is the incident photon's wavelength.
w1 - w0
=h (1-cos (b))/ m ec
That is :
w1 - w0
=Wc(1-cos (b))
Where Wc= h/ m ec
is known as the Compton wavelength.
4. Differential cross section for the Compton scattering
For an incident photon (x-rays, γ-rays) of energy Eγ, the differential
cross section is given by the Klein-Nishina formula:
dσ/dΩ = re2/2 {P - P2sin2θ + P 3}
Where:
P = P(Eγ,θ) = 1/[1 + (Eγ/mec2(1 - cosθ)]
re is the classical electron radius, me is the electron rest mass, θ is the scattering angle,
and dΩ = 2πsinθ dθ.
|