Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Radioactive decay
1. The law of the decay
Let N0 the population of radioactive nuclei at the beginning; that is
at the time t = t0.
At a time t = t, the short time after t = t0, the population
N0 decreases and becomes N(t).
The difference dN(t) = N0 - N(t) occurs at the time t = t,
after the time t0; that is during the period dt = t - t0.
Let's remark that dN is negative because N0 is greater than N(t).
The ratio: - dN(t)/dt is called the Activity of the substance; that is the
population decay rate. It is the rate at which the process occurs. In other
words, it is the rate at which the desintegration occurs.
In The SI, the activity is measured in becquerel (Bq); that is the number
of desintegration (or emission)per second.
The ratio: - dN(t)/N is called the fractional reduction of the population. It
means also the percentage of population reduction. It is
proportional to the time dt. Let's write:
- dN(t)/N = λ dt (1)
λ is called the decay constant or the desintegration constant.
Solving for N(t), the integration gives:
ln[N(t)] = - λt + Constant
Or:
N(t) = K exp (- λt)
Where the constant K = exp (Constant)
Solving for K, we have:
At t = t0, N(t) = N0
the equation (1) can be written then:
N0 = K exp (- λt0)
Hence:
K = N0exp (λt0)
N(t) = K exp (- λt)
K = N0exp (λt0) (2)
In the case of t0 = 0, K = N0.
N(t) = N0 exp (- λt)
N0 = N(0) (3)
2. Other expression of the activity
Deriving the relationship (2), we obtain:
A = - dN(t)/dt = K λ exp (- λt) = λ N(t) = A0exp (- λt)
With A0 = K λ
A(t) = A0 exp (- λt) (4)
3. The half-time of a sample
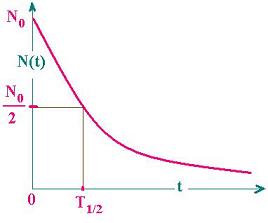 The half-time T1/2 is the time at which
the population falls off by a half (by a
factor 1/2).
The half-time T1/2 is the time at which
the population falls off by a half (by a
factor 1/2).
Let's write:
N(T1/2) = N(0)/2 = N0/2
N0exp (- λT1/2) = N0/2
Hence:
1/2 = exp (- λT1/2); and And:
λT1/2 = ln 2
That is:
T1/2= (ln 2)/λ (3)
4. The rate of the acticity
From the relationship (1), the rate of the acticity is
expressed by:
R = - dN(t)/N dt = λ
Or from the relationship (4), it takes the expression:
R = - dA(t)/A = λ
λ is also the rate at which the population
decays regarding the initial population.
Rate of activity = λ
|