Nuclear fission and fusion processes

Radioactivity is a nuclear spontanous reaction without any intervention. Other nuclear reactions such as fission and fusion are artificial. The fission process is the splitting of a nucleus to form two smaller ones, while fusion is the fusing of two smaller atoms to form a larger one.

1. Fission:

Fission is concerned by heavy nuclei. In such process, a nucleus, with large number of nucleons, captures one neutron, and splits into two fragments with smaller number of nuleons, followed by the emission of one or more neutrons. The two obtained fragments have a low binding energy per nucleon; then they are more stable regarding the initial nucleus. The fission process deals essentially with U(235,92), U(233,92) Uranium atoms, and P(239,94) Plutonium atom. The neutron (without electric charge) approches a nucleus without being deviated from its direction by electrostatic interactions. Those that have low kinetic energy (≈ 0.1 eV corresponding to the energy of a neutrons at ambient temperature), are more likely to produce the 235-Uranium nucleus fission. They are called thermal neutrons. Fission is a nuclear process which requires incident neutrons to start the reaction. Each produced neutron will produce one or more others; therefore nuclear chain reaction will takes place. This process does not last for a long time. It liberates a strong quantity of energy in a very shorttime that is an explosion such as in an atomic bomb (bomb A). In nuclear reactors, the fission process, escially the neutron emission rate, is controlled.

The reaction for one atom 235-Uranium is the following:
U(235,92) + n → Xe(139,54) + Sr(95,38) + 2n.
The number of charge is always conserved. The energy liberated by the reation is ε = (m_i - m_f) c²

We have for the individual masses:
U(235,92): m_U = 234.993 uma
Xe(139,54): m_Xe = 138.914 uma
Sr(95,38): m_Sr = 94.856 uma
n: m_n = 1.009 uma

Then:
m_i = m_U + m_n
m_f = m_Xe + m_Sr + 2m_n

m_i - m_f = m_U - m_Xe - m_Sr - m_f = 0.215 uma (about 0.1% of the initial 235-Uranium is transformed in energy).
Then: ε ≈ 0.215 x 1.66 x 10 ^-27 x 9 x 10¹⁶ ≈ 3.2 x 10 ^-11 joules. This energy is find in most part as kinetic energy for the produced nucleus, the rest is taken by the neutrons and γ rays.

For one mole, we have: E = Na ε = 6.023 x 10 ²³ x 3.2 x 10 ^-11 ≈ 2 x 10¹³joules, which is an enourmous energy quantity!.

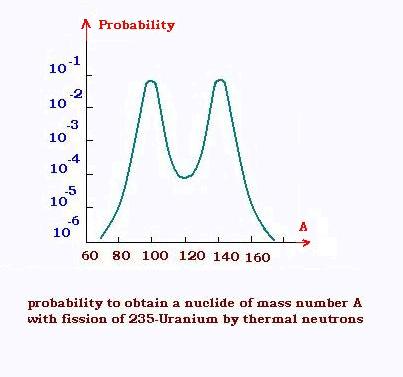
The products of the fission process are very large for a same initial nucleus. This is due to the multiplicity of the fission modes and the decaying transformations of the produced nucleus. For the 235Uranium, we can have also the reation

U(235,92) + n → Ba(139,56) + Kr(94,36) + 3n .

Generally, the probability to obtain nuclei by fission looks like the 235-Uranium probability distribution profile by thermal neutrons, shown at right. This crve is slightly modified when the captured neutrons are more energetic. The fission of the 239-Plutonium and the 233-Uranium gives similar results. The 239-Plutonium is an artificial element. It is produced by the capture of a neutron of high kinetic energy (rapid neutron) of the order of some MeV by the 238-Uranium, followed by the emission of two electrons (β^-). By an identical process, the 232-Thorium leads to the 233-Uranium via a protactinium (Pa) by the following series:

Th(232,90) + n → Th(233,90), then:
Th(233,90) → Pa(233,91) + e^-, and:
Pa(233,91) → U(233,92) + e^-

The 232-thorium nad the 238-Uranium are relativeley abundant in nature. The 232-thorium leads to the 233-Uranium and the 238-Uranium leads to the 239-Plutonium. Both of the two products are fissile. We say that the 232-thorium and the 238-Uranium are fertile.
The Uranium in nature is composed of 0.72% of 235-Uranium fissile and 99.27% of 238-Uranium fertile.The 238-Uranium is not fissile, but it is converted to the 239-Plutonium which is fissile as the 235-Uranium and the 233-Uranium.

2. Fusion:

In the process of fusion, two light atoms and combine to form a heavier atom, followed or not by emission of aparticle such as neutron, electron, positron, proton, ... .
For example, the reaction prduced in the sun is:
H(1,1) + H(2,1) → H2(3,2)
As for a fission, a fusion reaction conserves the bumber of nucleons and the number of charge.

The energy liberated by this reaction is: ε = (m_i - m_f) c²
We have for the individual masses:
H(1,1): m₁ = 1.0073 uma
H(2,1): m₂ = 2.0134 uma
H(3,2): m₃ = 3.015 uma
Then:
m_i - m_f = m₁ + m₂ - m₃ = 5.79 x 10 ^{- 3} uma ε ≈ 5.79 x 10 ^{- 3} x 1.66 x 10 ^-27 x 9 x 10¹⁶ ≈ 8.65 x 10 ^-13 joules = 5.4 MeV.

The fusion is favored when the binding energy per nucleon of the final nucleus is greatre than the ones of the initials nucleus.
For the reaction: Li(7,3) + H(1,1) → Be(8,4),
where the binding enrgy per nucleon for the Lithium is ε_Li = 5.4 MeV and for the Beryllium ε_B2 = 6.8 MeV; the liberated enrgy is calculated as follows:
We separate first the 7 nuclons of the Beryllium that requires the enrgy E_Li = 7 x ε_Li = 7 x 5.4 = 37.8 MeV.
Next, reconstitute the Be(8,4) from 8 nucluons (7 for Li(7,3) plus 1 for H(1,1)), that requires the energy E_Be = 8 x ε_Be = 8 x 6.8 = 54.4 MeV. Hence the energy liberated by the reaction is: E_Be - E_Li = 54.4 - 37.8 = 16.6 MeV.

To realise this the initial nucleons must very energetic in order to overcome the strong repultion electric forces between the positive charges of these nucleons. Hence the fusion requires nucleons with high kinetic energy (≈ 1 MeV). The temperature of a medium increases with respect to the kinetic energy of the constituting particles; therefore, the fusion is possible only at temperature about one billion degrees ^oC; that we call the thermonuclear fusion.

The fusion is spontaneous within stars. Artificially, on earth, these high temperatures conditions could be reproduced by an explosion of a bomb A. This can triggers the reaction:
H(2,1) + H(3,1) → He(4,2) + n ,
wich is the principle of the bomb H. For One kilogram of the initial charge of fusion (Deuterium and Tritium combined), the energy liberated is on the order of produced by 200 kilo-tons of TNT (Trinitrotoluene).

The fusion releases much more energy per mass compared to the fission. In other words, the energy liberated from 1kg of 235-Uranium as fuel is less than that one from the fusion of 1kg of Deuterium and Tritium combined. Currently, the related research focuses on obtaining high temperature (at least some tens of millions degrees) plasma or using lasers to experiment the theortically possible fusion reaction.