Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Quantum theory
1. Planck law has the form of Wien's formula
We car rewrite the Planck law this way:
u(ν, T) = (8πh/c3) ν3 /(exp{hν/kT} - 1)
= (8πh/c3) T3 (ν/T)3 x 1 /(exp{h/k) (ν/T} - 1)
That is exactly the form set by Wien; that is:
u(ν,T) = T3 f(ν/T), with f(ν/T) = (8πh/c3) x (ν/T)3 x 1 /(exp{h/k) (ν/T} - 1)
2. Approximations in Planck law
2.1. hν/kT >> 1
We can then neglect the term 1 in (exp{hν/kT} - 1), then:
u(ν, T) = (8πh/c3) ν3 exp{ - hν/kT}
2.2. hν/kT << 1
In this cas:
exp{hν/kT} - 1 = 1 + (1/!1) hν/kT + (1/!2) (hν/kT)2 + ... - 1
≈ hν/kT
We have seen that:
E = hν/(exp{hν/kT} - 1)
Then:
E = hν/(exp{hν/kT} - 1) = hν/hν/kT = kT
We find the classical value of the average energy of an
oscillator. This value was used by Rayleigh and Jeans, using
the energy equipartition principle.
Remarks:
1. h is not null, because that leads to 0/0 ( indetermination.
If we tend h towards 0, we find E = kT
2. For any temperature value; if h tends to infinity, then
u(ν, T) tends to 0; which is not possible because there is
certainly a radiation inside the cavity, since it is heated.
(ex → 0 when x → 0)
3. The ratio hν/kT has no dimention. (or is the unity); then
the dimension of h is [kT/ν] = energy/frequency = joules.second ;
that action.
4. h is really a constant because k is the constant (Boltzmann) and
ν/T is constant (Wien displacement).
5. h is called Planck constant.
The dimension of h is the action = joules . seconds
Now, what is the value of the constant h?
3. Value of the h constant
3.1. Planck results
3.1.1. Planck curves
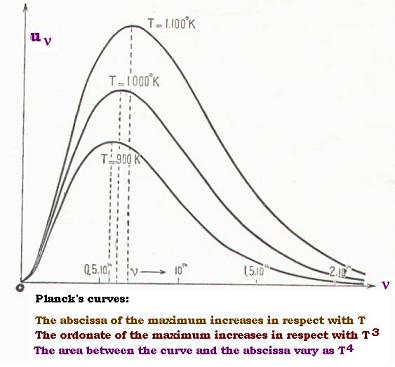
Following the resluts of Planck, we have:
Scale: 3.85 cm corresponds to 1014 sec-1
νm is the frequency of the maximum in sec-1
νm/T in 1010 x sec-1 x oK-1
x = distance from 0 to νm in cm.
3.1.2. Measurements
| T(oK) | x | νm | νm/T |
| 90 | 2.12 | 0.55 | 6.11 |
| 1000 | 2.20 | 0.57 | 5.70 |
| 1100 | 2.51 | 0.651 | 5.92 |
We get an average vallue for νm/T , which is:
νm/T = 17.73 x 10(10/3
νm/T = 5.91 x 1010 sec-1 x oK-1
3.2. Value of h/k
The abscissa of a maximum, for a given temperature T, νm, is obtained
by the zero of the derivative of the function u(ν, T); that is:
du(ν,T) = 0; which gives:
d[(8πh/c3) ν3 /(exp{hν/kT} - 1)] = 0
= (8πh/c3) d[ν3 /(exp{hν/kT} - 1)].
d[x3/(ex - 1)] = 0 → 3x2(ex - 1) - x3ex = 0
That is : (x/3) + e - x = 1.
By successive approximation, the numerical value of this equation is xm = 2.826
Then:
hνm/kT = 2.826
With νm/T = 5.91 x 1010 sec-1 x oK-1,
we have:
h/k = 0.478 x 10-10 sec.oK
We have also in the wavelengths scale:
u(λ, T) = (8πhc/λ5) x 1/(exp{hc/λkT} - 1)
du(λ,T)/dλ = 0 → (8π(kT)5/(hc)4) d[x5/(ex - 1)]/dλ = 0
with x = hc/λkT
d[x5/(ex - 1)]/dλ = 0
gives:
(x/5) + e-x = 1
With successive approximations, we find xm = 4.965
We have then:
hc/λmkT = 4.965 ; thus: λmkT/c = 0.2014 h
With:
hνm/kT = 2.826, and
λmkT/c = 0.2014 h
we obtain with the product:
hνm/kT x λmkT/c = 2.826 x 0.2014 h = 0.569; that is:
νm x λm/c = 0.569
or:
(νm/cT) x λmT = 0.569
with c= 3.0 x 1010 cm/sec
νm/T = 5.91 x 1010 sec-1 x oK-1
we get:
λmT = 0.288 cm.oK
λmT = 0.288 cm.oK
3.3. Total energy density
The spectral energy density is the Planck law. The total spectral energy
density is the Stefan law; indeed:
U = U(T) = ∫ u(ν,T)dν [ν : 0 → + ∞ ] =
u(ν, T) = (8πh/c3) ∫ ν3 /(exp{hν/kT} - 1) dν
∫ ν3 /(exp{hν/kT} - 1) dν =
∫ (kT/h)4 x (hν/kT)3 /(exp{hν/kT} - 1) d(hν/kT)
= (kT/h)4 ∫ (hν/kT)3 /(exp{hν/kT} - 1) d(hν/kT)
x = hν/kT → ∫ x3/(ex - 1) dx [ν : 0 → + ∞ ]
= π4/15 = 6.494
Then:
U = U(T) = (8πh/c3) x (kT/h)4 x π4/15 =
(8π5/15c3h3) k4 t4
That we can write U = aT4; that is the Stefan law.
We had seen that the blackbody total emissive power is written by:
P = (c/4) U(T) = σ T4 ; and the value of the constant
σ = ac/4 is measured and it is equal to 5.67 x 10 -5 erg.sec-1.cm-2.oK-4.
σ = 2π5k4/15c2h3 = 5.67 x 10 -5
With c = 3.0 x 1010 cm/sec, we have:
k4/h3 = 0.125 x 1016 erg.sec3.oK4
k4/h3 = 0.125 x 1016 erg.sec- 3.oK- 4
3.4. The value of h
The following product gives the value of h:
h = (h/k)4 x (k4/h3) = [0.478 x 10-10]4 x 0.125 x 1016
[sec.oK]4 . erg.sec- 3.oK- 4 erg.sec.
= 6.53 x 10- 27 erg.sec
h = 6.53 x 10- 27 erg.sec
That is the value of the Planck constant.
3.5. Deduced constants from h
The value of h gives the value of the Boltzmann constant R/Na = k;
where R is the ideal gas constant and Na is the Avogadro number:
h/k = 0.478 x 10-10 sec.oK, then:
k = h/0.478 x 10-10 erg.sec / sec.oK = 1.368 x 10-16 erg.oK-1
k = 1.368 x 10-16 erg.oK-1
Then:
Na = R/k = 8.314 x 107/1.368 x 10-16 (erg.mol-1oK-1)/(erg.oK-1)
= 6.06 mol-1
Na = 6.06 mol-1
The advantage here is that the ideal gas constant is easily measured according
to PV = nRT (or PV = RT for a mol gas) law for the ideal gases.
Next, the electron charge constant:
The Faraday number is equal to 96500 = Na x e Coulomb. mol-1
(wher Na is the Avogadro number and e is the electron charge). We have then:
e = F/Na = 96500/6.06 = 1.59 x 10-19 Coulomb
e = 1.59 x 10-19 Coulomb
The advantage here is that the Faraday constant is easily measured according
to electrolysis experience.
4. Validation of the Planck constant h
At this related time,Wien, Rayleigh and Jeans were theoritician deside
Ernst Pringsheim and Otto Lummer that were experimenters had been working
on the blackbody issues.
Pringsheim and Lummer measured the blackbody spectral intensity E(λ,T).
According to the Planck formula and that E(λ,T) = (c/4π) u(λ,T);
we can write:
E(λ,T) = (c/4π) u(λ,T) = (L/λ5) x 1/(exp{P/λT} - 1)
where L = 2hc2 and P = hc/k are constants.
Here are their results:
4.1. Pringsheim and Lummer curves
For a constant temperature T corresponds a curve E(λ,T) with respect
to λ. By repeating the same measurements for different temperatures, we
obtain the following isotherm curbes:
4.2. Measurements and results
scale: 1.35 cm for λ = 2µm
We have then:
λm = 1.92 µm at T = 1500 oK
λm = 2.30 µm at T = 1250 oK
Thus:
λmT = 2885 µm.oK = 0.2885 cm.oK
(that is the Wien displacement).
If we write: P/λT = x, we can have:
E(λ,T) = Constant. x5/(ex - 1). We have seen that the
zero-derivative of x5/(ex - 1) leads to: xm = 4.965
Then:
P = λm T . 4.965 = 1.432 cm.oK.
For the constant L, we have to use the Stefan constant:
We have:
σ = 2π5k4/15c2h3 = 5.67 x 10 -5 CGS
And:
L = 2hc2, P = hc/k . Thus: σ = (π5/15) x (L/P4).
That gives the value of L = 1.185 x 10-5 CGS
With c = 2.997 x 1010 cm/sec, we find:
h = 6.55 x 10-27 CGS. That is the value found by Planck at 1%.
5. Actual value of the constant h
Precise experiments on the blackbody emission gives the
following values:
λmT = 0.2898 cm.oK
h = 6.626 x 10-34 J.sec (joule.second)
Then:
k = 1.380 x 10-23 J/oK
R = 8.314 J.oK-1 .mol-1
Na = 6.022 x 10o23 mol-1
F = Na e = 96485.81 Coulomb.mol-1
e = 1.602 x 10-19 Coulomb
We use often ℏ = h/2π = 1.0545 x 10-34 Joule.sec
And also ℏc = 197.328 Mev.Fermi, with 1 eV = 1.6 x 10-19 joules
and 1 Fermi = 1 x 10-15 meters
|
