Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
The NMR
1.Larmor frequency: The precession of the proton
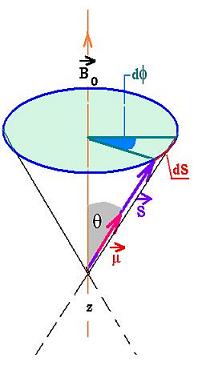
In the absence of am external magnetic field, the magnetic
moment of spin are oriented randomly in space. When an
external magnetic field is applied, the magnetic moment of spin μ
will tend to align with the field, as shown in the folowing figure:
The manetic moment of spin is extended from the definition of
the angular magmetic momemt. Applyied for the electron, we have:
μe-/orbit = -eL/2me (1)
Where L is the angular momentum for the electron
Then:
μe-/spin = -geS/2me (2)
Where S is the spin angular momentum for the electron
g is called the Lande factor
g = 2.00232 for the electron
For the proton, let's write:
μp/spin = egS/2mp (3)
g = 5.58569
The torque for the angular momentum is that
the force is for the linear momentum. We define the
vector torque τ applyied for the spin magnetic moment μ in a
magnetic field B0 as:
τ = μ x B0 = μ B0 sinθ (4)
Where &theta is the angle between μ and B0.
Since dφ is small, We can write :
dS = S sinθ d&phi (5)
The variation of S in time can be written as:
τ = dS/dt = S sinθ dφ/dt
Using the equatios: (4) and (3), we get: (6)
τ = μ B0 sinθ = egS/2mpB0 sinθ
Using (6) we get:
dφ/dt = eg/2mpB0 (7)
Let's write this expression as follow:
ω0 = eg/2mpB0
= γB0 (8)
Where γ = eg/2mp, (9)
called Gyromagnetic ratio.
Or ƒ0 = ω0/2π = eg/4 π mpB0
Which is called the Larmor frequency.
The two possibles values of S are :
ms = +1/2 or ms =-1/2
The related energy for each state is :
E-1/2 = - μB0 (opposite the direction of the field : high energy).
E+1/2 = + μB0 (same as the direction of the field : low energy).
The difference is:
Δ = 2 μB0 = ħω
(according to the Planck relationship. ħ = h/2π , h is the Planck constant.)
Then:
ω = 2 μB0/ħ (10)
We have the two following values for b = 1 Tesla (10,000 Gauss):
ω = 2.67 x 108 s-1
ƒ = 42.58 MHz
2. NMR: The principle
NMR stands for Nuclear Magnetic Resonace. That is
the effect of the spins is efficient only in the case of the
external frequency Ω is in the order of ω0 (Larmor):
Ω ≈ ω0.
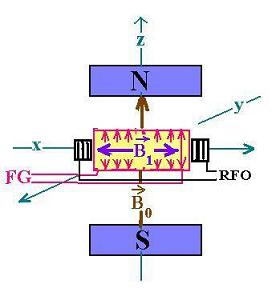In this figure:
The sample to study is set inside the coil receiving the RF.
. B0 is the first magnetic field applyied.
. B1 is the second magnetic field generated
by FG: the frequency generator (Radiofrequency input)
. This field oscillates over the x axis.
. RFO is the radiofrequency output. It is the signal to
analyse by the imaging technique using Fourier transform
to deal with frequencies instead of time variable, that is
the MRI ( Magnetic Resonance Imaging).
3. The Bloch Equations:
The magnetization M0 of the substance is the average of
all the spin magnetic moments of each atom μi. We write:
M0= Σμi which is pointed along of the z axis.
The second field B1(t) exerts a second torque
on the moment M0 leading it to the y axis, as shown below:
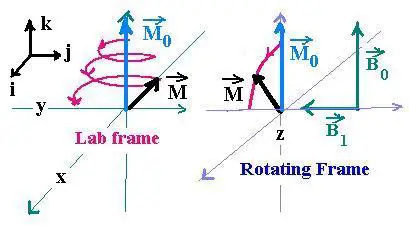The Bloch equations explain the evolution of the magnetization moment
during its precession. Since the magnetic field B1(t) is
time dependant, so is the magnetization moment: M(t).
In the frame laboratory the magnetization vector M rotates
about y abd about z axix.
In the rotating frame the magnetization vector M rotates
about y axis.
Let's consider that the field B points toward certain
direction.
We have for the proton:
τ = μ x B = dS/dt (11)
From (9) and (3), we have:
γ S = μ
Then the relationship ( 11) becomes:
dμ/dt = μ x γB
The summation of μ over a unit volume gives:
dM/dt = M x γB (12)
That is M precesses about B with a frequency equal to ω = γB
This is the first equation of Bloch.
The important phenomenun related to the evolution of the
Magnetization vector is its relaxation following the
precession induced by the excitation.
Two relaxations occur: the longitudinal relaxation and the transverse relaxation.
3.1. The longitudinal relaxation
The longitudinal component of the magnetization M behaves
as follow:
dMz/dt = - (Mz - M0)/T1 (13)
The solution of this equation is :
Mz = M0 + (Mz(0)- M0)e-t/T1
Since Mz(0) = 0 ( at 90o), we have then:
Mz = M0 ( 1- e-t/T1) (14)
T1 is called the spin-latice time constant. It
characterizes the return to equilibrium along the z-direction.
3.2. The transverse relaxation
It behaves according to :
dMxy/dt = - Mxy/T2 (15)
Since Mxy(0) = M0, the solution of this equation is:
Mxy = M0 e-t/T1 (16)
T2 is called the spin-spin time constant and characterizes
the decay of the transverse nuclear magnetization.
Combining the equations (12), (13) and (15), the general
Bloch equation becomes:
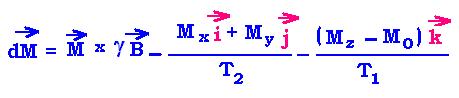The first term of the above equation can be written as:
dM/dt = (MyγB0, - MxγB0, 0)
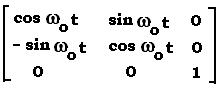The solution of the Bloch equation is:
M(t) = T Ry(ω0t) M0 + (0, 0, M0 ( 1- e-t/T1) )
Where:
Ry(ω0) is the rotation matrix about z.
M0 = (0,0, M0)
T = I.(e-t/T2, e-t/T2, e-t/T1)
where I is the 3x3 unit matrix.
In the rotating frame, we can write:
Mrot(t) = (0, Mroty, Mrotz) = (0, M0sin ωt, Mrotcos ωt)
The first term from the Bloch equation can be written:
dMrot/dt = Mrot x γ Beff
Where Beff = Brot - ω/γ
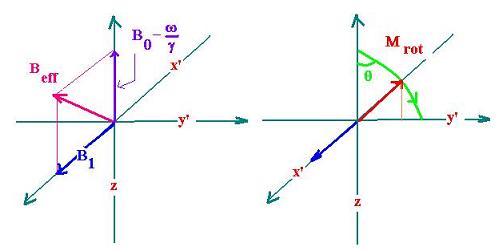The Bloch equation is the same in the two references, but
in the rotating frame Beff influences Mrot.
|
