Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Rutherford scattering
1. The description of the collision
The main idea, here is the discovery of the proton.
Geiger and Marson experimented the collision of
α particles (of energy 5.5 Mev) from the Radon Rn(222,86);
that is the nuclei of the He(4,2) incident on the gold Au(197,79)
target (of width 10-6m = 1 µm).
Geiger and Marson found about 1 on 104 α are returned
back (scattered in the direction θ>π/2).
J.J. Thomson had thought; that is the
the atom was like a pulm ( or raisin) pudding, where the pudding was
positive charges and raisin electrons. This is the first atomic model
that it doesn't work at all.
With the rutherford experiment, It came out that the incident particles
had a small amount of deflections and even some particles returned from
the target.
The conclusion was that the atom is made up of the positive nucleus and
electrons where the biggest part is simply a vacuum. This second model
gave a good understanding about the atom.
Features of the collision:
Projectile:
m : Mass of the projectile
vi : Initial speed of the projectile
vf : Final speed of the projectile
Z1e : Charge : (Z : atomic number, e : electron charge)
Pi : Momentum
Ni : Number of incident (alpha) particles
T = (1/2)mvii2 : kinetic energy of projectile ( a )
Pi = mvi : initial momentum
Li = mvib : initial angular momentum
Lf = mvfb : initial angular momentum
Eα = E i = (1/2) mvi2 : The kinetic energy
of the incident particle
Eα = (1/2)mvi2
Target nuclei:
M : Mass of the target
Z2e : Charge
Pf : Final momentum
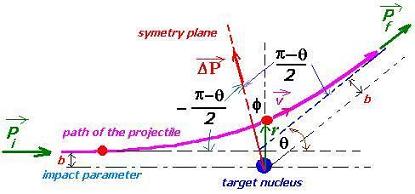
Detection parameters:
ε0 : Permittivity of space
θ: Scattering angle
φ : The angle between the vector position and
ω = dφ/dt : The angular velocity of the particle at any moment
the axis of the hyperbola
r : Position vector; the radial unit vector (||r|| = 1).
d : Target-to-detector distance
L = mvr = mωr2 : Angular momentum at any moment
b : Impact parameter
The scattering under the influence of the Coulomb force involve the
dependence of the scattering θ angle and the impact parameter b which
is the crucial parameter for nuclear scattering.
We Consider the M>>m. So,the magnitudes of the initial and final
momenta are the same considering their conservation and the assumption
that the target recoil is negligible:
Let:
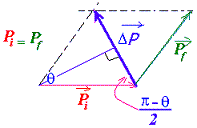
ΔP = ||ΔP|| = ||Pf - Pi|| = 2 mvi sin(θ/2) (1)
The Coulomb vector force is expressed by:
F = (1/4πε0) Z1Z2e2 r/r2 (2)
r : is the position of the projectile from the target at any moment.
In view of the symmetry of the scattering geometry, the net change of this force is
located in the symmetry axis of the hyperbola. Therefore:
FΔP = F cos φ (3)
Recall that F = dP/dt; hence : P = ∫ F dt.
And L:the angular momentum is conserved; that is Li = Lf = L = mvr = mωr2;
Li = L gives: mvib = mωr2
Hence:
r2/vib = 1/ω = dt/dφ (4)
We have then:
ΔP = ∫FΔP dt ( from -&infinit to +&infinit)
= ∫F cos φ dt ( from : - (π-θ)/2 to + (π-θ)/2)
= ∫dφF cos φ (dt/dφ)
= ∫dφF cos φ(r2/vib)
= (Z1Z2e2/4πε0vib) &int:cos φdφ ( from : - (π
-θ)/2 to + (π-θ)/2)
= (Z1Z2e2/4πε0vib) . 2 cos(θ/2) (5)
Equating the relationships (1) and (5) we get:
b = (Z1Z2e2/4πε0mvi2) ctg(θ/2)
Since Eα = (1/2) mvi2, we have then:
b = (1/2)(Z1Z2e2/4πε0 Eα) ctg(θ/2) (6)
Let's write :
rc = (Z1Z2e2/4πε0) x 1/ Eα
That is obtained with φ = 0 and b = 0
In this case, the kinetic enrgy of the incident particle is
null; wheras the potential energy takes the expression:
Ep = Z1Z2e2/4πε0rc
Recall that the size of the nucleus is given by the formula :
rnucleus = 1.2 A 1/3. Where A is the mass of the nucleus
For the gold element A = 197, thus rnucleus = 8 fm
For the current Rutherford collision : rc ≈ 30 fm
and the Bohr radius ≈0.5 105 fm
The expression of the impact parameter takes then the form:
b = (rc/2) ctg (θ/2) (7)
wich is the Rutherford formula.
2. The related cross section
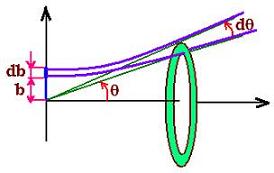
The differential cross section gives information about
the probability for the insident α to be scattered
in a certain direction.
The total cross section is expressed by:
σ = π b2 (8)
Then:
dσ = 2π b db
dΩ = 2πsinθdθ
dσ = 2π b db sinθdθ / sinθdθ = dΩ b db / sinθdθ
Where Ω is the related solid angle.
Hence;
dσ/ dΩ = (b / sinθ)(db /dθ) (9)
From the equation (7), we get:
|db / dθ| = rc/2 . (1/2 sin2(θ/2) (10)
The equation (9) becomes:
dσ/ dΩ = (rc/2 ctg(θ/2)/sinθ) / rc/2 . (1/2 sin2(θ/2)
(11)
With sin θ = 2 sin(θ/2) cos&(θ/2), we find:
dσ/dΩ = (rc/4)2 1/sin4(θ/2)
|