Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Thompson scattering
1. Introduction
The scattered radiation cross section varies with respect to the scattered
angle. It shows where is probable to find a scattered radiation.
An electromagnetic wave propagates carrying two fields wich are its components.
They are the electriv field, E and the magnetic fiel B. The vectors corresponding to
these fields are perpendicular to each other and to the direction of the propagation
(the poynting vector).
When an electromagnetic wave is incident on a charged particle, its electric and
magnetic components exert a Lorentz force on the particle. The incident wave varies
(is periodic) in time, so is the exerted force. Once the particle is accelerated, It
emits, in its turn, a radiation.
In other words, the energy lost by the incident wave is gained (absorbed) by the particle
target, setting it in a motion. This particle reemits this energy as electromagnetic
radiation. This process is called scattering of the electromagnetic wave by the particle.
Two processes could occur: The exchange of energy is inelasctic (the emitted wave has not
exactly the same energy as the incident wave, the difference is used by the electron to
recoil). This is called Compton Scattering. If the exchange of energy is elasctic,
the emitted wave has exactly the same energy (the same frequency) as the incident wave).
The related process is called Thompson Scattering.
2. Thompson scattering
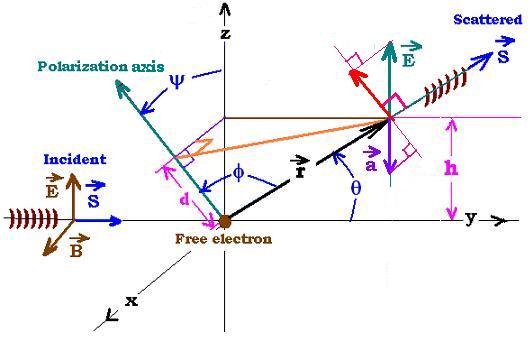 We consider the approximation of small velocities, so the magnetic component of the Lorentz
force is neglected. The particle undergoes only the electric field effect, thus the equation
of motion of the charged particle is approximately : f = q E. Also the particule is assumed to
be free electron (that is its binding enery is less than the enegy hν of the incident photon).
We consider the approximation of small velocities, so the magnetic component of the Lorentz
force is neglected. The particle undergoes only the electric field effect, thus the equation
of motion of the charged particle is approximately : f = q E. Also the particule is assumed to
be free electron (that is its binding enery is less than the enegy hν of the incident photon).
We have two particular cases:
2.1. The wave is polarized:
Consider a linearly polarized, monochromatic, plane wave (El, B) incident on a
particle (free electron). If the polarization is set over the z axis, the field E will remain
parallel to z axis (vertical), so is the acceleration of the target electron (because F = q E).
We know that the direction of the radiated electric field E is given by r x (r x a) ("r" is
the position vector of the electric field from the charge). Hence the scattered wave will move
from un element of scattering volume, in the plane (x,y), all over the z axis. The electric field
of the scatterd wave will remains parallel to the incident field. The field El
points towards a direction perpendicular to the palne (x,z). As it depends on the time, It will
oscillate vertically over the an axis parallel to the z axis. The remitted (scattered) radiation
wave goes in the "y" direction.
2.2. The general case:
Now the incident radiation is not polarized (or randomly polarized). Then the acceleration of
te particle target takes any direction in the space. So is its electric field E. For any direction
of the incident field in space, we have the acceleration "a" that points in any direction. So is
the corresponding electric field (Ea). For a given angle θ in the plane (y,z),
the electric filed E will points in direction of its polarization vector P. The vextor P is
in the (x,z) plane. The angle between r and P is φ (φ = π/2 - θ) that takes
all the values from 0 to 2π around the x axis. Plus, for one value of φ we have to take
all directions in the plane (x,z); that is all the possible values of the angle ψ,
from 0 to 2π.
The calculation of the angular distribution of the scattering radiation cross section
will have the following steps:
For each angle θ we consider all values fo the angle
φ for all values of ψ.
We can write:
r projected over z axis gives h = r sin θ. Projected again over the polarization
axis, gives d = r sin θ cos ψ. But this value is equal to r cox φ
Thus:
cox φ = sin θ cos ψ (1)
3. Differential cross section of the Thompson scattering
Let's write:
Eint = E0 sinωt , the expression of the incident electrical field.
The vector electric field E is parallel to the z-axis; it becomes E cos θ in order to be
perpendicular to the wave vector "r". For the related scattered electromagnetic wave,
the electric field has the following expression:
Eout = (e/4πε0r c2) a cos θ = (e/4πε0r c2) a sin φ;
where "a" is the acceleration of the particle = ∂s/∂t, and s is any displacement of this
particle from the origin, "e" is the charge of the particle (the electron), and m is its mass.
The equation of motion of the charged particle is: m a = e Eint = e E0 sin ωt
Hence: a = (e/m) E0 sin ωt (2)
The time average of each Poynting vector for the two electric fiels are:
Sint = c ε0 <Eint2> = c ε0 E02 <sin2ωt>
Sout = c ε0 <Eout2>
We have :
sin2x = (1-cos2x)/2
then :<sin2x>= ∫dx (1-cos2x)/2 /∫dx = 1/2 (3)
The integration is set from 0 to 2π
Thus:
Sint = c ε0 E02/2 (4)
Sout = c ε0 (e/4πε0)2 <a2> <sin2φ>/c4 r2
From the equations (2) and (3), we get <a2> = (1/2) (e E0/m)2
<sin2φ> = ∫dψ sin2φ /∫dψ [ψ: from 0 to 2π] = (1/2π) ∫dψ (1 - cos2φ)
Using the formula (1), we have:
∫dψ cos2φ = ∫dψ cos2ψsin2θ = sin2θ ∫dψ cos2ψ
∫dψ cos2ψ = ∫dψ (1/2 + cos 2ψ) = π
Hence:
<sin2φ> = (1/2π)(2π - π sin2 θ) = (1 + cos2θ)/2 (5)
Then:
Sout = c ε0 (e/4πε0)2) .(1/2) (e E0/m)2/ c4 r2 . (1/2)(1 + cos2θ)
= (e2 E0) 2 (1 + cos2θ) /4(4π)2ε0 c3 r2 m2
The differential scattering cross section per electron is given by:
dσTh/electron = Sout dA /Sinc
Where dA is the elementary surface = dV/dr = r2 2π sinθdθ = r2 dΩ
Thus:
dσTh/electron = Sout r2 dΩ /Sinc
dσTh/electron/ dΩ = r2 Sout /Sinc
We have:
Sout /Sinc = (e2/4πε0 m c2)2 (1/r)2 ( 1 + cos2θ)
Let: re = e2/4πε0 m c2 = 2.8 x 10-15 m, the classical electron radius . Hence:
Sout /Sinc = (1/2) (re/r)2 ( 1 + cos2θ)
Finally:
dσ/dΩ (Thomson-Electronic) = (re2/2)(1 + cos2θ) (6)
Which is the differential scattering cross section with respect to the
solid angle: dΩ = 2πsin θdθ. This differential cross section depends only on the angle θ.
5. Total cross section
The total scattering cross section is:
σTotal = ∫dΩ (dσTh/electron/dΩ) = (2π) (1/2) (re2) ∫( 1 + cos2θ), from 0 to π
.
= π(re2) ∫( 1 + cos2θ) = ( 2 + 2/3) π re2
dσ/dΩ (Total) = (8π/3)re2 ≈ 6.65 X 10-29 m2 (7)
dσTh/electron/ dΩ = dσTh/electron/ 2πsin θdθ
dσTh/electron/ dθ = 2πsin θdσTh/electron/ dΩ = 2πsin θ (1/2) (re)2 (1 + cos2θ)
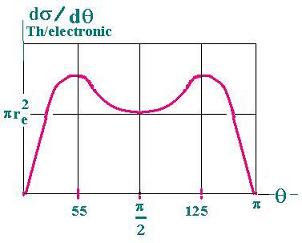
dσ dθ (Thompson/electron) = π (re)2 sin θ (1 + cos2θ)
Where:
re = e2/4πε0 m c2 = 2.8 x 10-15 m
The function dσ dθ (Thompson/electron) presents two maxima (at 550 and 1250) and a
minimum for 900 as shown below:
|