Contents
The nucleus
Radioactivity
Radiation Measurements
Black body radiation
Statistical Mechanics
Radiation and scattering
Related topics
Related links
© The scientific sentence. 2010
|
Black body's radiation
Blackbody spectral energy distribution
1. The experimental result
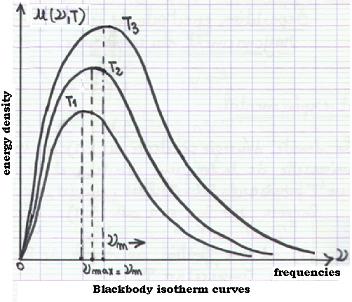
The spectral energy density u(λ,T) is an universal function
of the wavelength λ and the teperature T as it is the specific
spaectral intensity E(λ,T).
With ν = c/λ, we have: u(λ, T) = (ν/c2) u(λ,T)
u(ν,T) is an universla function of the frequency ν and the temperature T.
The main issue, regarding the study of the blackbody rays in the
determination of this universal function. The Stefan law is not
sufficient to show all the needed blackbody features.
The experimental results have shown that the profile of the enrgies emitted
from a blackbody cavity related to monochromatic radiations, for a given temperature,
is a "bell curve". The set of all this profiles is known as the blackbody isotherms.
2. Wien displacement law
Since λ = c/ν, we have dλ = (c/ν2) dν
The energy of the radiation is written as:
W(λ) = (ν2/c) W(ν) or W(ν) = (λ2/c) W(λ)
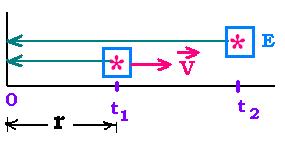
Now, leT 's consider a signal emitted at the time t1 from an emitter E moving at the velocity v.
For the observer, this signal reaches the point 0 at the time t1' = t1 + r/c
If another signal is emited at the time t2 by the emitter, it will reach the point 0 at
the time t2' = t2 + (t2 - t1)v/c + r/c.
We have then : t2' - t1' = t2 - t1 + (t2 - t1)v/c = (t2 - t1)( 1 + v/c).
If the signal is a radiation of period t2 - t1; this period measered in the fixed
frame 0 is t2' - t1'. Assuming that v << c, forethermore, the
frequency of the radiation is 1/(t2' - t1') = 1/(t2' - t1')(1 + v/c) = (1 - v/c)(t2' - t1'). With
ν' = 1/(t2' - t1') and ν = 1/(t2 - t1), we have ν' = ν(1 - v/c), known as Doppler
effect.
LeT 's write dν = ν' - ν. We have then:
dν/ν = - v/c
We assume that radiation takes place inside a volume V with reflecting (adiabatic)
faces that if they contract or expand the compression remains an isentropic
process (the entropie S is constant). From the relationship (13.3), if we differentiate
S = (4/3) a T3, we find: dS = 0 → dV/V + 3dT/T = 0
dV/V + 3dT/T = 0
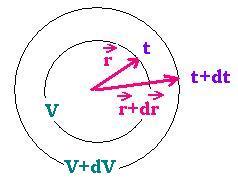
We consider that the volume V is expanded by dV from r to r+dr. During the time
interval dt, between r and r + dr, a point on the cercle of the volume V moved to
the cercle of the volume V+dV with a velocity v = dr/dt. The radiation travelled, during the
ng the same
interval of time dt, the distance r + dr = c dt. We can write :
(r + dr)/c = dr/v. As dr << r, we have then:
dr/r = v/c
With the Doppler effect,V = (4/3)πr3, and from the
relationship dV/V + 3dT/T = 0, we have dν/ν = - v/c = - dr/r = - (1/3) dV/V = dT/T
dν/ν = dT/T
Integrating the above equality, we find ν/T = constant, especially
at the maximum:
νmax/T = constant
Wien's displacement law
3. Wien formula
LeT 's consider a frequency interval Δ ν that becomes
by an isentropic process,Δ ν'. We can write:
d(Δ ν)/Δ ν = dT/T.
The Stefan formula u = a T4, where u is the energy
density per volume unit, gives du/u = d(Δu)/Δu = 4dT/T
The energy density u depends on λ or ν and T. We can write:
du = u(ν,T)dν then Δu = u(ν,T) Δν.
It follows that:
d(Δu)= du(ν,T)Δν + u(ν,T) d(Δν).
Dividing by u(ν,T)Δν , we have:
d(Δu) /u(ν,T)Δν = du(ν,T)/u(ν,T) + d(Δν) Δν
or:
4dT/T = du(ν,T)/u(ν,T) + d(Δν) Δν + dT/T
thus:
du(ν,T)/u(ν,T) + d(Δν) Δν = 3dT/T
Integrated becomes:
du(ν,T) = T3 f(ν,T)
f(ν,T) is a function depending on ν and T.
If we integrate for all the frequencies, we have to
find the Stefan law:
U = aT4 = ∫ du(ν,T)dν [ν: 0 → + ∞ ]
We have:
U = aT4 = ∫ du(ν,T)dν = ∫ T3 f(ν,T) dν
or:
aT4 = ∫ T3 f(ν,T) dν = T4 ∫ f(ν,T) dν/T
Hence:
The constant a = ∫ f(ν,T) d(ν/T) and f(ν,T) has to be
written as: f(ν,T) = f(ν/T). Then:
u(ν,T) = T3f(ν/T)
That is the Wien formula
But this function will remains unknown.
4. Conclusion
In a black body cavity at a temereture T, the frequency of a radiation
ν chnage into ν' when the temperature change into T '; but
the ratio ν/T = ν'/T ' = Constant.
The specral energy density u(ν,T), or the energy of transported by a radiation of
frequency ν at the temerature T, per volume unit becomes u'(ν',T ') and we
have, according to the Stefan law:
u(T ') /u(T) = (T '/T)4
And according to the Wien formula, we have:
u(ν',T ')/u(ν,T) = (T '/T)3 f(ν'/T ')/f(ν/T)
Since f(ν'/T ') = f(ν/T), we have:
u(ν',T ')/u(ν,T) = (T '/T)3
Then:
ν' = (T '/T)ν
u(T ') = u(T)(T '/T)4
u(ν',T ') = u(ν,T) (T '/T)3
The set of the isotherm curves of u(ν,T) is build from the single
function u(ν,T) by a translation of the abscissa ν to ν' = (T '/T)ν
and the ordinate u(ν,T) to u(ν',T ') = u(ν,T) (T '/T)3 simultanously.
We will have the same results with λ = c/ν:
We have: u(λ,T) = (ν2 /C) u(ν,T) = (c/λ2) u(ν,T)
According to Wien formula:
The: u(λ,T) = (c/λ2) T3 f(ν/T) = (c/λ2) T3 f(c/λT)
As we have ν/T = constant; we have also λT = constant. That is:
λ' = (T/T ') λ
Hence: f(c/λT) = f(c/λ'T ') = constant
Thus:
u(λ',T ') = (λ/λ')2 (T '/T)3 u(λ,T)
= (T '/T)2 (T '/T)3 u(λ,T) = (T '/T)5 u(λ,T)
λ' = (T/T ') λ
u(λ',T ') = (T '/T)5 u(λ,T)
The set of the isotherm curves of u(λ,T) is build from the single
function u(λ,T) by a translation of the abscissa λ to λ' = (T/T ')λ
and the ordinate u(λ,T) to u(λ',T ') = u(ν,T) (T '/T)5 simultanously.
|