least squares function 

1. Definition:

In the least squares method, the sum of the distances between the observed 
(yi) and calculated (f(xi, pi))values must be minimum. 
The square of this distance is equal to l2 = yi - f(xi, pi), 
and the sum is L2 = ∑ (yi - f(xi, pi)). That's the value we minimize with 
respect to the parameters pi.

In the case of a linear function, f(xi, pi) is written as 
a x + b, and the related parameters are the slope (a) and the y_intercept (b).

To draw an approximative linear equation of type y = a x + b, that 
should give the best fit for the drawn data points, we need to know 
its slope (a) and its y_intercept (b).

  
  
  
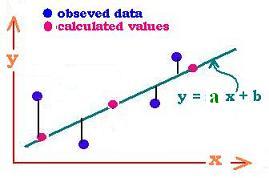Here, we show how to calculate the slope and the y_intercept 

2. The program in C language:


	#include <stdio.h>
	#include <math.h>


	int get_number()
	{
	int num;
	printf("\n How many points will you represent ?: --> ");
	scanf("%d", &num);
	return num;
	}


	int main()
	{
	int num = get_number();

	float abscissas[num];
	float ordinates[num];


		printf("\n Enter their x_coordinates:\n");
	int i;
	for (i = 0; i<num; i++)
	{
	scanf("%f", &abscissas[i]);
	}

		printf("\n Enter their corresponding y_coordinates:\n");
	int j;
	for (j = 0; j<num ;j++)
	{
	scanf("%f", &ordinates[j]);
	}


	float x1=0.0,y1=0.0,x2=0.0,xy=0.0;
	float num_slope, deno_slope, slope=0.0;
	float num_intercept, deno_intercept,intercept=0.0 ;

		for ( i = 0; i <= num - 1; i++)
		{
		x1 += abscissas[i];
		y1 += ordinates[i];
		x2 += abscissas[i] * abscissas[i];
		xy += abscissas[i] * ordinates[i];
		}

	num_slope = num*xy - x1*y1;
	deno_slope = num*x2 - x1*x1;

	if (deno_slope == 0){
		printf("\n The denominator is zero. \n");
	}
	else
	{
	slope = num_slope/deno_slope;
	}


	num_intercept = x2*y1  - x1*xy;
	deno_intercept = num*x2 - x1*x1;

	if (deno_intercept == 0){
		printf("\n The denominator is zero. \n");
	}
	else
	{
	intercept = num_intercept/deno_intercept;
	}
		printf("\n The slope is : %2.2f, and the y_intercept is %2.2f . \n", slope, intercept);
		printf("\n");
	if (intercept<0)
		printf("\n The related linear equation is: y = %2.2f x %2.2f \n", slope, intercept);
	else
		printf("\n The related linear equation is: y = %2.2f x + %2.2f \n", slope, intercept);

	return 0;
	}