1. D�finitions:
Un cycle thermodynamique sur une machine est
un ensemble de procesus effectu�s de telle sorte
que le syst�me revient � son point de d�part.
Dans ce cas toutes les variations des variables d'etat comme l'energie
interne, l'enthalpie, et l'entropie, au cours du cycle sont nulles:
ΔU = U(final) - U(initial) = U(initial - U(initial) = 0.
De m�me ΔH = 0 et ΔS = 0
D'apr�s le premier prinicipe Q - W = ΔU pour un syst�me
ferm�, ou Q - W = ΔH pour un syst�me ouvert, On a:
Wcycle = Qcycle.
Cel� veut dire que la mchine, au cours du cycle ne garde
rien pour elle; elle est juste le si�ge de transformations.
Le rendement d'une machine, comme tout rendement, est le rapport
entre ce que la machine nous donne et ce qu'on lui donne.
On peut l'ecrire: η = Fourni/Re�u .
Une machine thermique doit fonctionner avec deux sources de
chaleur, une chaude Qc et une froide Qf. Au cours d'un cycle, la
machine recoit Qc et rejette Qf, tout en ne gardant rien pour elle.
Au cours de ce cycle Qcyle = Qc - Qf. Cette diff�rence
est �gale au travail net Wnet = Wcycle extrait de la machine.
Le travail est net, puisqu'on doit tenir compte d'un travail qui
peut �tre donn� � la machine, donc re�u par elle. On peut ecrire
Wnet = Wfourni - Wre�u
Wfourni = fourni par la machine, Wre�u = re�u par la machine
Nous ecrivons:
η = Wcycle (net)/Qc(re�ue) = (Wfourni - Wre�u)/Qc
= Qcycle/Qc = (Qc - Qf)/Qc = 1 - (Qc/Qf)
Retenons:
η = Wcycle(net)/Qc = (Qc - Qf)/Qc
Remarque: Dans le r�f�rentiel du
syst�me, Qf est toujours n�gative. Dans ce cas, il s'agit
bien de Qc - |Qf|
2. Le cycle de Carnot:
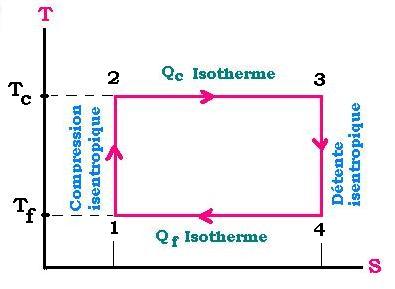 Tc est la temp�rature de la source chaude,
Tf est la temp�rature de la source froide.
Le processus 1-2 est une transformation isentrropique ΔS = 0.
C'est une compression qui �l�ve la temp�rature du syst�me de Tf � Tc.
Le processus 2-3 est une transformation isotherme acompagn�e d'un
apport de chaleur Qc qui permet de garder cette temp�rature Tc
constante et �gale � la temp�rature de la source chaude le long
de ce processus 2-3.
Le processus 3-4 est une transformation isentrropique ΔS = 0.
C'est une d�tente qui baisse la temp�rature du syst�me de Tc � Tf.
C'est en ce moment que le syst�me fourni du travail � l'ext�rieur.
Le processus 4-1 qui ferme le cycle est une transformation isotherme
acompagn�e d'un rejet de chaleur Qc qui permet de garder cette
temp�rature Tf constante et �gale � la temp�rature de la source froide
le long de ce processus 4-1.
Nous avons:
ΔS(1-2) = S2 - S1 = 0
ΔS(2-3) = S3 - S2 = Qc/Tc → Qc = Tc(S3 - S2)
ΔS(3-4) = S4 - S3 = 0
ΔS(4-1) = S1 - S4 = Qf/Tf → Qf = Tf(S1 - S4) qui
est n�gatif; d'une part.
D'autre part, ΔS(2-3) = - ΔS(4-1)
C'est � dire:
Qc/Tc = - Qf/Tf → Qf/Qc = - Tf/Tc → |Qf|/Qc = Tf/Tc
Le rendement de cette machine id�ale est :
η = (Qc - |Qf|)/Qc = 1 - (|Qf|/Qc) = 1 - (Tf/Tc)
Tc est la temp�rature de la source chaude,
Tf est la temp�rature de la source froide.
Le processus 1-2 est une transformation isentrropique ΔS = 0.
C'est une compression qui �l�ve la temp�rature du syst�me de Tf � Tc.
Le processus 2-3 est une transformation isotherme acompagn�e d'un
apport de chaleur Qc qui permet de garder cette temp�rature Tc
constante et �gale � la temp�rature de la source chaude le long
de ce processus 2-3.
Le processus 3-4 est une transformation isentrropique ΔS = 0.
C'est une d�tente qui baisse la temp�rature du syst�me de Tc � Tf.
C'est en ce moment que le syst�me fourni du travail � l'ext�rieur.
Le processus 4-1 qui ferme le cycle est une transformation isotherme
acompagn�e d'un rejet de chaleur Qc qui permet de garder cette
temp�rature Tf constante et �gale � la temp�rature de la source froide
le long de ce processus 4-1.
Nous avons:
ΔS(1-2) = S2 - S1 = 0
ΔS(2-3) = S3 - S2 = Qc/Tc → Qc = Tc(S3 - S2)
ΔS(3-4) = S4 - S3 = 0
ΔS(4-1) = S1 - S4 = Qf/Tf → Qf = Tf(S1 - S4) qui
est n�gatif; d'une part.
D'autre part, ΔS(2-3) = - ΔS(4-1)
C'est � dire:
Qc/Tc = - Qf/Tf → Qf/Qc = - Tf/Tc → |Qf|/Qc = Tf/Tc
Le rendement de cette machine id�ale est :
η = (Qc - |Qf|)/Qc = 1 - (|Qf|/Qc) = 1 - (Tf/Tc)
Cycle de Carnot (cycle parfait ou id�al)
ηcarnot = 1 - (Tf/Tc)
2. Le cycle de Brayton:
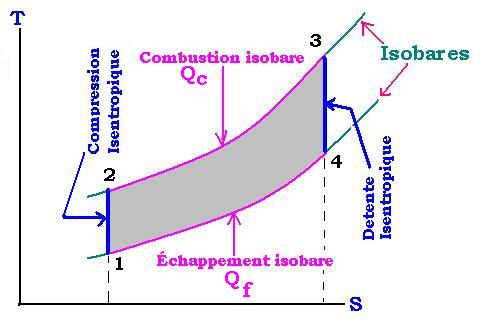 Cette machine est constitu�e d'un compresseur (1-2), d'une
chambre de combustion (2-3)qui apporte une quantit� de chaleur
QC, d'une turbine (3-4) qui recuille le travail fourni, et d'un
dispositif d'echappement refroidissant Qf.
On d�signe par &taux; le taux de compression de la machine, c'est
� dire lors du processus de compression (1-2) P2 = τ P1 et
lors du processus de d�tente (3-4) P3 = τ P4.
Cette machine est constitu�e d'un compresseur (1-2), d'une
chambre de combustion (2-3)qui apporte une quantit� de chaleur
QC, d'une turbine (3-4) qui recuille le travail fourni, et d'un
dispositif d'echappement refroidissant Qf.
On d�signe par &taux; le taux de compression de la machine, c'est
� dire lors du processus de compression (1-2) P2 = τ P1 et
lors du processus de d�tente (3-4) P3 = τ P4.
Processus 1-2: au niveau du compresseur:
Le gaz (air) est compress�, sa temp�rature s'�l�ve de T1 � T2 et
sa pression s'el�ve de P1 � P2.
Le processus est isentropique (adiabatique et reversible), donc:
Q = 0 → W = - ΔH = - CpΔT
W(re�u) = - ΔH = - CpΔT
Le processus �tant adiabatique:
T2 = T1[P2/P1](γ - 1)/γ
ΔT = T2 - T1, donc
T2 - T1 = T1[[P2/P1](γ - 1)/γ - 1]
ou, avec τ = P2/P1
T2 - T1 = T1[[τ](γ - 1)/γ - 1]
et
W(re�u) = - CpΔT = - Cp(T2 - T1)
Processus 2-3: au niveau de la chambre de combustion:
La combustion se fait � pression constante; le processus est
isobare P2 = P3. Sous l'effet de la chaleur re�ue Qc, la
temp�raure de proc�d� (air) s'�l�ve de T2 � T3. Nous avons:
Qc = CpΔT = Cp(T3 - T2)
Processu 3-4: au niveau de la turbine:
Le temp�rature baisse de T3 � T4.
Le processus est adiabatique (puisque c'est isentropique),
donc
Q = 0 → W = - ΔH = - CpΔT
W (fourni)= - CpΔT
avec ΔT = T4 - T3
W (fourni)= - Cp(T4 - T3)
T4 = T3[P4/P3](γ - 1)/γ
donc T4 - T3 = T3[[P4/P3](γ - 1)/γ - 1]
ou
T4 = T3[1/τ](γ - 1)/γ
T4 - T3 = T3[[1/τ](γ - 1)/γ - 1]
Processus 4-1 au niveau du refroidissement:
Durant le processus 4-1, qui est isobare, le gaz est
refroidi en c�dant une quantit� de chaleur Qf. Nous avons
Qf = CpΔT = Cp(T1 - T4)
T1 - T4 = T1 - T3[1/τ](γ - 1)/γ
Rendemant de la machine:
Le rendement de cette machine est :
η = W(net)/W(re�u)= [W(re�u)- |W(fourni)|]/W(re�u)
Re�u au niveau du compresseur et fourni au niveau de
la turbine.
W((net) = W(re�u) - W(fourni) = - Cp(T2 - T1)+ Cp(T4 - T3)
η = [- Cp(T2 - T1) + Cp(T4 - T3)]/ [- Cp(T2 - T1)] =
η = 1 - [|(T4 - T3)|/(T2 - T1)]
η = 1 - {T3[[1/τ](γ - 1)/γ - 1 / T1[[τ](γ - 1)/γ - 1]}
Connaissant T1 et T3 , on peut calculer T2 et T4
Connaissant le taux de compression P2/P1 = τ = P3/P4
On peut par cons�quent calculer η
On peut aussi verifier que:
η = (Qc - Qf)/Qc = 1 - (Qf/Qc) =
1 - [ Cp(T1 - T4)/Cp(T3 - T2)]
= 1 - [|(T1 - T4)|/(T3 - T2)]
Sous form compacte:
η = 1 - {T1 - T3[1/τ](γ - 1)/γ} /
{T3 - T1[τ](γ - 1)/γ}
= 1 - [[1/τ](γ - 1)/γ]{T1[τ](γ - 1)/γ - T3} /
{T3 - T1[τ](γ - 1)/γ}
= 1 - [[1/τ](γ - 1)/γ]{T1[τ](γ - 1)/γ - T3} /
{T3 - T1[τ](γ - 1)/γ}
= 1 - [[1/τ](γ - 1)/γ]
ηbrayton =
1 - [[1/τ](γ - 1)/γ]
Application:
Si T1 = 20 oC, T3 = 1200 oC, γ = 1.4, et τ = 10, alors:
η = 1 - [[1/10](1.4 - 1)/1.4] = 1 - 0.52 ≈ 48%
1. Le cycle d'Otto:
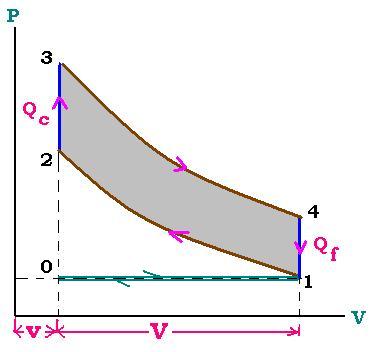 Le moteur � combustion interne � quatre temps, comme
celui d'une voiture, fonctionne sous ce cycle.
Le point 0 est appel� le point mort haut: PMH
Le point 1 est appel� le point mort bas: PMB
Tc est la temp�rature de la source chaude,
Tf est la temp�rature de la source froide.
Le taux de compression volumique τ = (V + v)/v
V = volume pendant la course du piston
v = volume de la chambre de combustion
1. Le temps 0-1:
Le piston dans le cylindre descend du PMH au PMB
en aspirantle m�lange air-essence, son volume augmente
de v � V de fa�on isobare.
2. Le temps 1-2:
Le gaz est comprim� de fa�on adiabatique et r�versible,
le volume du cylindre diminue de (V + v) � v, sa
pression augmente de P1 � P2, et sa temp�rature augmente
de T1 � T2.
On a donc Q = 0 → W = - ΔH = - Cp
ΔT = - Cp (T2 - T1) =
P1V1γ = P2V2γ
P2 = P1 (V1/V2)γ = P1[(V + v)/v]γ =
P1 τγ
P2 = P1 τγ
T2/T1 = (V1/V2)γ - 1 =(P2/P1)(γ - 1)/γ
T2 = T1 [(v + V)/v]γ - 1 = T1 [τ]γ - 1
T2 = T1 [τ]γ - 1
3. Le temps 2-3:
La combustion �tant isochore, donc la chaleur fourni aux
gaz est Qc = ΔU = Cv ΔT = Cv (T3 - T2)
D'o� T3 = Qc/Cv + T2
Comme P3/P2 = T3/T2, donc: P3 = P2 (T3/T2) = P1 τγ (T3/T2)
P3 = P1 τγ (Qc/T2Cv + 1)
P3 = P1 τγ [(Qc/(T1 [τ]γ - 1)Cv) + 1]
4. Le temps 3-4:
Les gaz se d�tendent en fournissant un travail m�canique.
La pression diminiue et le volume augmente. La transformation est
adiabatique r�versible:
T4/T3 = (V3/V4)γ - 1 = [v/(V + v)]γ - 1 =
[1/τ]γ - 1
T4 = T3[1/τ]γ - 1
On P3V3γ = P4V4γ
Donc:
P4 = P3 (V3/V4)γ =
= P3 [v/(V + v)]γ = P3 [1/τ]γ
5. Le temps 4-1:
Le syst�me c�de de la chaleur � l'exterieur.
Qf = CvΔT = Cv (T1 - T4) = Cv (T1 - T3[1/τ]γ - 1)
6. Le temps 1-0:
Les gaz d�gagent � l'atmosph�re de fa�on isobareet le cycle
recommance.
Le moteur � combustion interne � quatre temps, comme
celui d'une voiture, fonctionne sous ce cycle.
Le point 0 est appel� le point mort haut: PMH
Le point 1 est appel� le point mort bas: PMB
Tc est la temp�rature de la source chaude,
Tf est la temp�rature de la source froide.
Le taux de compression volumique τ = (V + v)/v
V = volume pendant la course du piston
v = volume de la chambre de combustion
1. Le temps 0-1:
Le piston dans le cylindre descend du PMH au PMB
en aspirantle m�lange air-essence, son volume augmente
de v � V de fa�on isobare.
2. Le temps 1-2:
Le gaz est comprim� de fa�on adiabatique et r�versible,
le volume du cylindre diminue de (V + v) � v, sa
pression augmente de P1 � P2, et sa temp�rature augmente
de T1 � T2.
On a donc Q = 0 → W = - ΔH = - Cp
ΔT = - Cp (T2 - T1) =
P1V1γ = P2V2γ
P2 = P1 (V1/V2)γ = P1[(V + v)/v]γ =
P1 τγ
P2 = P1 τγ
T2/T1 = (V1/V2)γ - 1 =(P2/P1)(γ - 1)/γ
T2 = T1 [(v + V)/v]γ - 1 = T1 [τ]γ - 1
T2 = T1 [τ]γ - 1
3. Le temps 2-3:
La combustion �tant isochore, donc la chaleur fourni aux
gaz est Qc = ΔU = Cv ΔT = Cv (T3 - T2)
D'o� T3 = Qc/Cv + T2
Comme P3/P2 = T3/T2, donc: P3 = P2 (T3/T2) = P1 τγ (T3/T2)
P3 = P1 τγ (Qc/T2Cv + 1)
P3 = P1 τγ [(Qc/(T1 [τ]γ - 1)Cv) + 1]
4. Le temps 3-4:
Les gaz se d�tendent en fournissant un travail m�canique.
La pression diminiue et le volume augmente. La transformation est
adiabatique r�versible:
T4/T3 = (V3/V4)γ - 1 = [v/(V + v)]γ - 1 =
[1/τ]γ - 1
T4 = T3[1/τ]γ - 1
On P3V3γ = P4V4γ
Donc:
P4 = P3 (V3/V4)γ =
= P3 [v/(V + v)]γ = P3 [1/τ]γ
5. Le temps 4-1:
Le syst�me c�de de la chaleur � l'exterieur.
Qf = CvΔT = Cv (T1 - T4) = Cv (T1 - T3[1/τ]γ - 1)
6. Le temps 1-0:
Les gaz d�gagent � l'atmosph�re de fa�on isobareet le cycle
recommance.
Le rendement:
η = 1 - (|Qf|/Qc) = 1 - |(Cv (T1 - T4)|/Cv (T3 - T2)) =
Qf/Qc = Cv (T1 - T4)/Cv (T3 - T2 = (T1 - T3[1/τ]γ - 1)/
(T3 - T1 [τ]γ - 1)
= [1/τ]γ - 1 (T1[τ]γ - 1) - T3)/
T3 - T1 [τ]γ - 1)
= [1/τ]γ - 1 (-1)
Donc:
|Qf|/Qc = [1/τ]γ - 1
Donc:
ηotto = 1 - (1/τ)γ - 1
Application:
T1 = 20 oC, P1 = 1 bar, Qc = 1800 kJ/kg et τ = 9
Pour l'air, on a: Cp = 1.004 kJ/kg oK et
R = 0.287 kJ/kg oK et γ = 1.4
On trouve:
T2 = T1 [τ]γ - 1 = (20 + 273) 90.4 =
705.6 oK
T3 = Qc/Cv + T2 = Qc/(R - Cp) + T2 = 1800/(1.004 - 0.287) + 705.6 =
3216.1 oK
T4 = T3[1/τ]γ - 1 = 3216.1 (1/9)0.4 =
1335.5 oK
Qf = CvΔT = Cv (T1 - T4) = (1.004 - 0.287)(20 + 273 - 1335.5) =
-747.5 kJ/kg
ηOtto = 1 - (1/τ)(γ - 1) =
58.5 %
1. Le cycle de Diesel:
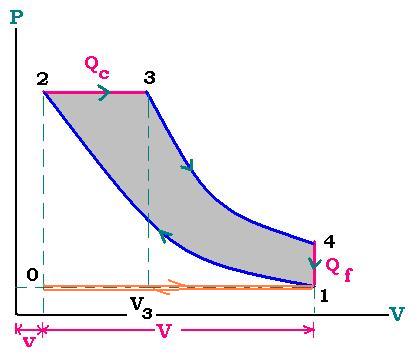 Le cycle de Diesel op�re de la m�me fa�on que le
cycle d'Otto, sauf au niveau de la combustion, c'est
� dire au niveau du processus 2-3 o� la chaleur re�ue
Qc se fait � isobare = pression constante. l'expression du
rendement est exactement la m�me, qui est ici fonction de Cp.
Nous avons:
P2 = P3
Le volume change de V2 � V3
Qc = ΔU = Cp ΔT = Cp (T3 - T2)
D'o� T3 = Qc/Cv + T2
Le taux de compression volumique τ(3-4) � la d�tente est
le rapport de V3 et V4 tels que:
La loi des gaz parfaits avec V4 = V1 et P2 = P3 donne:
V3 = RT3/P3 et V4 = V1 = RT1/P1 → V4/V3 = (T1/T3) x (P3/P1)
τ(3-4) = (T1/T3) x (P2/P1)
τ (1-2) est le taux de compression volumique pendant
la phase 1-2. τ(1-2) = P2/P1
Donc:
τ(3-4) = (T1/T3) x (τ(1-2))
Le rendement:
η = 1 - (|Qf|/Qc)
Le cycle de Diesel op�re de la m�me fa�on que le
cycle d'Otto, sauf au niveau de la combustion, c'est
� dire au niveau du processus 2-3 o� la chaleur re�ue
Qc se fait � isobare = pression constante. l'expression du
rendement est exactement la m�me, qui est ici fonction de Cp.
Nous avons:
P2 = P3
Le volume change de V2 � V3
Qc = ΔU = Cp ΔT = Cp (T3 - T2)
D'o� T3 = Qc/Cv + T2
Le taux de compression volumique τ(3-4) � la d�tente est
le rapport de V3 et V4 tels que:
La loi des gaz parfaits avec V4 = V1 et P2 = P3 donne:
V3 = RT3/P3 et V4 = V1 = RT1/P1 → V4/V3 = (T1/T3) x (P3/P1)
τ(3-4) = (T1/T3) x (P2/P1)
τ (1-2) est le taux de compression volumique pendant
la phase 1-2. τ(1-2) = P2/P1
Donc:
τ(3-4) = (T1/T3) x (τ(1-2))
Le rendement:
η = 1 - (|Qf|/Qc)
Application:
T1 = 15 oC, P1 = 1 bar, Qc = 2000 kJ/kg et τ = 21 (taux volumique)
Pour l'air, on a: Cp = 1.004 kJ/kg oK et R = 0.287 kJ/kg oK et γ
= 1.4
On trouve:
P2 = P1 τ(1-2)γ = 1 (21)1.4 = 70.97 bars
T2 = T1 [τ(1-2)]γ - 1 = (15 + 273)(21)0.4
= 973.4 oK
P3 = P2 = 70.97 bars (processus isobare)
T3 = Qc/Cp + T2 = (2000/1.004) + 973.4 = 2965.4 oK
τ(3-4) = (T1/T3) x (P3/P1) = (288/2965.4) x (70.97/1) = 6.893
P4 = P3 [1/τ(3-4)]γ = 70.97 x (1/6.893)1.4 =
4.76 bars.
T4 = T3 [1/τ(3-4)]γ - 1 =
2965.4 x (1/6.893)0.4 = 1370.0 oK
Qc = CpΔT = Cp (T3 - T2) = 1.004 x (2965.4 - 973.4) =
2000.0 oK
Qf = CvΔT = Cv (T1 - T4) = (Cp - R) ( T1 - T4) =
0.717 x (15 + 273 - 1370.0)= - 775.6 kJ
Le rendement:
η = 1 - (|Qf|/Qc) = 1 - 775.6/1992.0 = 61%
|