From the equation (3.2), the average force component <Fx> is:
<Fx> = <Ix>/ΔT
The pressure is then:
P = <Fx> /S = <Fx> /Ly. Lz
= <Ix>/ΔT /Ly. Lz =(m N ΔT/3Lx) <v2>/ΔT /Ly. Lz = m N /3V <v2>. Where the volume V is equal to Lx.Ly.Lz.
We find then:
PV = Nm<v2>/3 (3.4)
4.Internal energy and temperature
Let's consider a monoatomic gas whose molecules behave as a point
particles so that the potential energy between them is neglected. Plus, there are
no rotations nor vibrations related to the molecules; the internal energy
U of the system consists of the translational kinetic energy of the molecules
Ki; that is:
U = ΣKi = (1/2)m Σvi2 = (N/2)m <v2> = N <K>; (4.1)
<K> = Σvi2/N = (1/2)m <v2> (4.2)
is the mean value of the kinetic energy of the molecules.
We have U = ΣKi = N ΣKi/N = N <K> (4.3)
Combining (2.4) and (3.1), we get for an ideal gas: U = (N/2)m <v2> = (N/2)m 3PV/Nm = (3/2)PV = (3/2) nRT = (3/2) (N/NA)RT. Then:
U = (3/2)nRT = (3/2) NkT (4.4)
Where NA = 1.023 x 10 23 the Avogadro's number and k = R/NA = 1.38 x 10 - 23 T/K the Boltzmann Constant.
From the equations (3.1) and (3.4), we get:
<K> = (3/2) kT (4.5)
The root-mean-square of speed vrms is defined as:
vrms = [<v2>]1/2; that is by equating (3.2) and (3.5) :
vrms = [3kT/m]1/2
At very low temperature (T → 0); that gives vrms → 0 which means that
the molecules become at rest! That's incorrect, because the result is based on the Newton's laws
which do not adequately describe the motion of the molecules. Quantum Statistical Mechanics
must be used for a correct description of the molecular motion in gases.
Equipartition energy theorem
The average translational kinetic energy is given by the equation (4.5), that is : <K> = (3/2) kT = 3. [(1/2)kT]
the factor three comes from the fact that there are three translational degrees of freedom for each monoatomic molecule.
For an ideal gas the mean molecular mechanical energy <E> is the mean molecular kinetic energy <K>, that is
<E> = 3. [(1/2)kT]
The generalisation of this result is the equipartition of energy theorem
The average molecular mechanical energy <E> for a system of molecules at temperature T, with
each molecule having ν degrees of freedom is <E> = ν [(1/2)kT] (4.6)
<E> = ν [(1/2)kT] (4.7)
For a linear diatomic molecule, we have three translational degrees of freedom related to the motion of
the center of mass and two degrees of freedom corresponding to the rotation of the two atoms
around the two related perpendicular axes. We have: ν = 5. Adding two degrees of freedon regarding
the vibrational motion, we get, in the total ν = 7.
5. Molar heat capacities' relationship
For an ideal gas, at constant volume ( dV = 0).
According to the first law of Thermodynamis
, we have : dQ = dU = nCV dT (5.1)
For a monoatomic gas, from the equation (4.4), we have: U = (3/2)nRT ; then dU = (3/2)nR
Differentiating PV = nRT, we have PdV + VdP = nRdT (5.2)
Now, at contant pressure, dQ = nCPdT , and PdV = nRdT; then:
The 1st law gives:
dQ = dU + PdV = dU + nRdT (5.3)
For this isobaric process:
dQ = dU + nRdT = nCPdT, (5.4)
Since for an ideal gas, the internal energy depends only on the temperature,
for the same change in temperature, the change in inernal energy is the same for a constant volume and
for a constant pressure processes.
Substituting (5.1) in ( 5.4), we find: nCPdT = nCV dT + nRdT , then:
CV + R = CP.
R = CP - CV
(5.5)
For an ideal gas:
We know from the equation (3.4) that for an ideal gas U = (3/2) nRT,then
dU = (3/2) nRdT.
As dU = nCVdT,then CV = (3/2)R and CP = (3/2)R + R = (5/2)R
For a diatomic and polyatomic gases, <E> = ν [(1/2)kT]. using N = nNA, we have
U = N <E> = nNAν [(1/2)kT]. Since NAk = R, we find:
U = n ν [(1/2)RT]; then
CV = (1/n) dU/dT = (1/2) νR.
This result is in a good agreement with the predictions of the kinetic theory, but solely at
low temperature.
For a solid with N atomes attached to each other with an ideal spring, no rotation can occur. The main
degrees of freedom that we have here are the 3 translational and the three vibrational. The internal energy
of the solid with N atoms is the sum of kinetic and potential erergies of vibration of the atoms.
We have ν = 6, then
CV = 3R
called the Dulong-Petit law.
6. Adiabatic process
An Adiabatic process stands for no change of energy between the systema and
its surrounding; that is dQ = 0. This process occurs rapidly enough so that the heat
added is negligible (compression of the fuel-air in the automobile engine).
For an ideal gas, according to the 1st law, an infinitesimal adiabatic process can
be written as:
dQ = dU + pdV = nCV dT + PdV = 0 (6.1)
Differentiating PV = nrT, we get:
PdV + VdP = nRdT
From the equation R = CP - CV and using the equation:
γ = CP/CV, we get:
PdV + VdP = n(CP - CV)dT = ndTCV(γ - 1)
= ndTCV γ - ndTCV
From the equation (6.1), PdV + VdP = ndTCV γ + PdV.
We get then:
VdP = ndTCV γ = - γPdV
dP/P = - γ dV/V
ln(P) = - γln(V) + Constant
ln(P) + γln(V) = Constant
ln(PVγ) = Constant (6.2)
For an ideal gas at an adiabatic process, we have :
PVγ = Constant
7. Maxwell-Boltzman distribution
Let's consider a function f whose argument is the velocity v = (vx, vy, vz) and that is
the product of three functions as follows:
f(v) = fx(vx). fy(vy). fz(vz) (7.1)
A partial derivative gives:
∂f(v)/∂vx = [∂fx(vx)/∂vx]. fy(vy). fy(vz) (7.2)
∂f(v)/∂vx = [∂f(v)/∂v]. [∂v/∂vx] (7.3)
∂v/∂vx = ∂[vx2 + vx2 + vx2]1/2/∂vx = (1/2) . 2 vx/v = vx/v (7.4)
The equation (7.2) becomes:
[∂f(v)/∂v]. vx/v = [∂fx(vx)/∂vx]. fy(vy). fy(vz) (7.2')
By deviding by f(v), we get:
[∂f(v)/∂v]. vx/v f(v)= [∂fx(vx)/∂vx]/fx(vx) (7.2")
Therefore:
[∂f(v)/∂v]/v f(v)= [∂fx(vx)/∂vx]/fx(vx)/ vx (7.5)
We have the same relationships about y and z components:
[∂f(v)/∂v]/v f(v)= [∂fy(vy)/∂vy]/fy(vy)/ vy (7.5')
and
[∂f(v)/∂v]/v f(v)= [∂fz(vz)/∂vz]/fz(vz)/ vz (7.5")
Rewrite (7.5):
[∂f(v)/∂v]/v f(v)= [∂fx(vx)/∂vx]/fx(vx)/ vx = Constant = a (7.6)
∂fx(vx)/fx(vx)= a . vx ∂vx
(7.7)
Integrating, we obtain:
ln[fx(vx)] = (1/2) a vx2 + Constant
Thus:
fx(vx) = exp [(1/2) a vx2 + Constant] = Constant exp [(a/2) vx2]
(7.8)
Normalizing the function fx(vx), we would get:
∫ fx(vx)∂vx = 1; which is never possible because
∫ exp [(a/2) vx2]∂vx diverge if a the constant "a" is positive. It
follows that the constant "a" must be negative. We change it by rewriting the constant "a" , " - a"
instead, with the constant "a" positive; Then:
fx(vx) = Constant exp [- (a/2) vx2] (7.9)
Normalizing, we have:
1 = Constant ∫ exp [- (a/2) vx2] dvx (- ∞ → ∞)
= Constant . 2. ∫ exp [- (a/2) vx2] dvx (0 → ∞)
Using the result: ∫ exp[- a x2]dx (0 → ∞) = I(0) = [π/4a]1/2
from the probability integrale, It follows that:
1 = Constant.2.[π/4(a/2)]1/2, Then
Constant = [a/2 π]1/2
(7.10)
We have then:
f(vx) = [a/2 π]1/2 exp [- (a/2) vx2]
(7.11)
Now, we will determine the constant a. Equating (3.2) and (3.5), we find:
<v2> = 3kT/m (7.12)
Using the distribustion of speeds , we can write:
<v2> = ∫ f(v) dv v2
From the equation (1.4), we have
<v2> = 3 <vx2> = 3 ∫ f(v) dv vx2
= 3 ∫ vx2 . fx(vx) fy(vy) fz(vz) dvx dvy dvz
= 3 [a/2 π]3/2 ∫ vx2 . exp [(a/2) vx2] . (2π/a)
= 3 [a/2 π]3/2 . [2 (π/4)(1/(a/2)3/2] . (2π/a) = 3/a (7.13)
Equating (7.12) and (7.13), we get:
a = m/kT
(7.14)
Using (7.11), he equation (7.1) becomes:
f(v) = [a/2 π]3/2 exp [- (a/2) v2]
since dv = v2 dv sinθ dθ dφ, we get e function depending solely in
the magnitude of the velocity, that is the speed:
f(v)dv = 4π [a/2 π]3/2 exp [- (a/2) v2] v2 dv
Let's write:
f(v) = 4π[m/2πkT]3/2 v2 exp [- (m/2kT) v2]
(7.15)
That is the Maxwell velocity distribution.
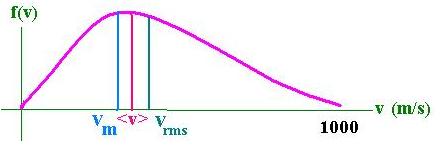 We want now to calculate:<v>, the average molecular velocity
We want now to calculate:<v>, the average molecular velocity
<v> = ∫ v f(v) dv = 4π[m/2πkT]3/2 ∫ v3 exp [- (m/2kT) v2] (0 → + ∞)
Since I(3) = 1/2a2, then:
<v> = (1/2) 4π[m/2πkT]3/2 (2kT/m)2 = [8kT/πm]1/2
<v> = [8kT/πm]1/2
Now, we want to calculate:vm, the more likely velocity for a molecule :
It is found by differentiating f(v) and to set it equal zero in order to find the maximum. It follows that:
df(v)/dv = 4π[m/2πkT]3/2 d[v2 exp [- (m/2kT) v2]]/dv = 0
2v exp [- (m/2kT) v2] - 2(m/2kT) v3 exp [- (m/2kT) v2] = 0
2v - 2(m/2kT) v3 = 0, that is: v2 = 2kT/m, therefore:
vm = [2kT/m]1/2
We can remark that :
vm < <v> < vrms