1. Définition:
|
Une turbine est une machine qui fourni un
fluide à haute pression utilisée pour produire un
travail mécanique.
Exemple:
Une turbine à gaz ou une turbine à vapeur.
Le procédé (fluide de travail) d'une turbine à gaz est généralement de
l'air; pour une turbine à vapeur, le procédé est généralement de l'eau.
|
2. Turbine à gaz, cycle théorique de Brayton
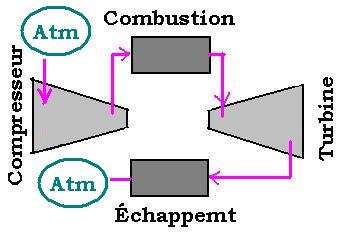
Elle comporte un compresseur
qui compresse l'air aspiré, une chambre de combustion
pour augmenter la température du mélange air-carburant, la turbine
qui receuille l'energie du gaz comprimé et chauffé afin de fournir
un travail mécanique, et enfin un un système d'échappement qui
rejette les gaz brûlés.
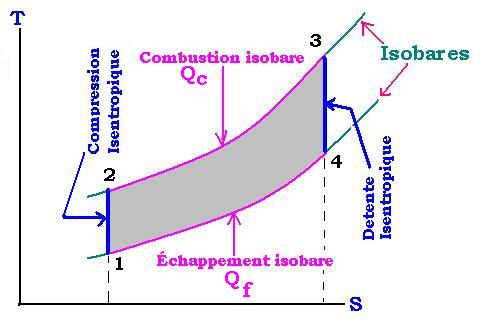
Une turbine à gaz est représentée par le diagrame de Brayton
dans un diagramme TS.
- Le processus 1-2 represente la compression isentropique.
- Le processus 2-3 represente la combustion isobare.
- Le processus 3-4 represente la détente isentropique.
- Le processus 1-2 represente l'échappement isobare.
Le rendement théoriquede cette machine a été calculé au chapitre II.
3. Turbine à gaz, cycle réel de Brayton
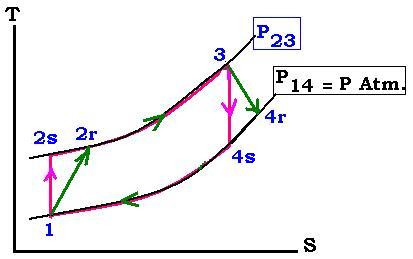
En réalité, le processus 1-2 et 3-4 ne sont pas isentropique (adiabatique
et réverible) à 100%. N'est pas adiabatique puisqu'une quantité non nulle de
chaleur est échangée avec le milieu extérieur; puis pas reversible puisque la
compresion, comme la détente, se font de façon brusque. Ainsi la correction à
apporter est que durant ces deux processus, d'ailleurs durant tous les processus
thermodynamiques pour un système isolé,l'entropie augment. Par conséquent, u
n décalage vers les entropies croissantes fait passer 2s en 2r et 4s en 4r. La compression
réelle et la détente réelle se font de façon irréversible, la combustion se fait de façon
quasi-isobare; le rejet des gas brûlés reste isobare à la pression atmosphérique.
Nous allons maintenant recalculer le rendement réel de la machine de Brayton. L'indice
"s" correspondra au processus isentropique (théorique) et l'indice "r" correspondra au
processus irreversible (réel).
Pour le compresseur:
ηCompresseur = ce qui est fourni par le gaz/ce qui est donné pour le gaz
= Travail isentropique /Travail réel
- Cp(T2s -T1)/- Cp(T2r - T1)
= (T2s -T1)/(T2r - T1)
ηCompresseur = (T2s -T1)/(T2r - T1)
- Cp(T2r -T1) est le travail réellement reçu par le système (gaz), donc négatif.
Ce travail comporte les pertes et le travail utile: - Cp(T2s - T1).
Pour la turbine:
ηTurbine = ce qui est fourni par la turbine /ce qui est donné à la turbine
= Travail réel/Travail isentropique
= + Cp(T4r - T3)/+ (Cp(T4s - T3)
ηTurbine = (T4r - T3)/(T4s - T3)
+ Cp(T4r - T3) est le travail réellement fourni par le système
(gaz dans la turbine), donc positif. La valeur de ce travail est inférieure à celle du travail
théorique qui ne contient pas les pertes de chaleur dans la turbine. Le travail théorique
+ Cp(T4s - T3) est plus grand que le travail réel + Cp(T4r - T3).
Donc:
ηCompresseur = (T2s -T1)/(T2r - T1)
ηTurbine = (T4r - T3)/(T4s - T3)
4. Applications
4.1. Application 1
T1 = 20 oC
P1 = 1 bar
T3 = 1200 oC
ηCompresseur = 80%
ηTurbine = 90%
Ï„ (taux de compression) P2/P1 = 10
On peut remarquer que le taux de compression théorique est égal au taux de
compression réel, puisque les processu 2-3 et 4-1 sont isobares. On parle
du taux de compression tout court.
On calcule T2s:
Le processus 1-2 étant idéal (isentropique), donc:
T2s = T1 [P2/P1](γ - 1)/γ
= (20 + 273)[10]0.4/1.4 = 565.67 oK ≈ 566 oK
T2s = 566 oK
On calcule T2r:
T2r = T1 + (T2s - T1)/ηCompresseur
= 293 + (566 - 293)/0.8 = 634.25 oK
T2r = 634.25 oK ≈ 634 oK
On calcule T4s :
On remarque que P1 = P4 = Patm et 2 3
et que P4/P3 = 1/Ï„
Le processus 3-4 étant idéal (isentropique), donc:
T4s = T3 [P4/P3](γ - 1)/γ
= (1200 + 273)[1/10]0.4/1.4 = 762.96 oK ≈ 763 oK
T4s = 763 oK
On calcule T4r:
T4r = T3 + (T4s - T3) x ηTurbine
= 1473 + (763 - 1473)x 0.9 = 834 oK
T4r = 834 oK
On calcule QC:
QC = + Cp (T3 - T2r)
= 1.004 x (1473 - 634) = 842.36
= 842.36 kJ/kg ≈ 842 kJ/kg
QC = + 842 kJ/kg
On calcule QF:
QF = - Cp (T1 - T4r)
= 1.004 x (293 - 834) = - 543.16 kJ/kg ≈ - 543 kJ/kg
QF = - 543 kJ/kg
On calcule ηCycle:
ηCycle = 1 -(|QF|/QC))
= 1 - (543/842) = 35.5 % ≈ 36%
4.2. Application 2
Un compresseur aspire de l'air à une température de 8 oC, avec
un débit de 1.25 kg/s; avec un rendement isentropique de 78%. Son taux de
compression est égal à 24. Les gaz brûlés entrent dans la turbine à
une température égale à 1050 oC. Le rendement isentropique de cette
turbine est de 86%.
On ecrit:
m (débit massique) = 1.25 kg/s
T1 = 8 oC = 281 oK
Ï„ (taux de compression) = 24
T3 = 1050 oC
ηCompresseur-S = 78%
ηTurbine-S = 86%
MACHINE THÉORIQUE:
1-2s: isentropique &arr;
T2s = T1 [P2/P1](γ - 1)/γ
= (8 + 273)[24]0.4/1.4 = 696.68oK ≈ 697oK
T2s = 697oK
le travail massique théorique fourni au compresseur = Wth-C = - Cp(T2s - T1)
= - 1.004 x (697 - 281) = - 417,343 ≈ - 417 kJ/kg
Wth-C = - 417 kJ/kg
3-4s: isentropique &arr;
T4s = T3 [1/τ](γ - 1)/γ
= (1050 + 273)[1/24]0.4/1.4 = 533.62 oK ≈ 534oK
T4s = 534oK
le travail massique théorique fourni par la turbine = Wth-T = - Cp(T4s - T3)
= - 1.004 x (534 - 1323) = + 792.16 ≈ + 792 kJ/kg
Wth-T (massique) = + 792 kJ/kg
Donc:
le travail massique net (la différence entre ce qui sort et ce qui rentre) théorique
de la machine est égal à:
Wth-NET = Wth-T - |Wth-C| = 792 - 417 = 375 kJ/kg
Wth-NET (massique) = 375 kJ/kg
On a:
Travail W = masse x (Travail Wmassique), donc la puissance
W = masse x (Travail Wmassique).
Ainsi, La puissance nette théorique est égale à:
Wth-NET = masse x Wth-NET (massique) = 1.25 x 375 = 468.75 ≈ 469 kJ/s
Wth-NET = 469 Watts
MACHINE RÉELLE:
ηCompresseur-S = (T2s -T1)/(T2r - T1) = 78%
T2r = T1 + (T2s - T1)/ηCompresseur-S
= 281 + ( 697 - 281)/0.78 = 814.33 oK ≈ 541 oC
T2r = 814.33 oK
le travail massique réel fourni au compresseur = Wré-C = - Cp(T2r - T1)
= - 1.004 x (814 - 281) = - 533 kJ/kg
Wré-C = - 533 kJ/kg
ηTurbine-S = (T4r - T3)/(T4s - T3) = 86%
T4r = T3 + (T4s - T3) x ηTurbine-S
= 1050 + 273 + ( 534 - 1050 - 273) x 0.86 = 644.46 oK ≈ 371.5 oC
le travail massique réel fourni par la turbine = Wré-T = - Cp(T4r - T3)
= - 1.004 x (644.46 - 1050 - 273 ) = + 681.25 kJ/kg
Wré-T (massique)= + 681.25 kJ/kg
Donc:
le travail massique net réel de la machine est égal à:
Wré-NET = Wré-T - |Wré-C| = 681.25 - 533 = 148.25 kJ/kg
Wré-NET (massique) = 148 kJ/kg
Ainsi, La puissance nette réelle est égale à:
Wré-NET = masse x Wré-NET (massique) = 1.25 x 328 = 410.3 ≈ 410 kJ/s
Wré-NET = 410 Watts
RENDEMENT DU CYCLE:
ηth = 1 - (P1/P2s)(γ - 1)/γ = 59.66 %
ηth = 60 %
La quantité de chaleur massique reçue par la chambre de combustion est Qc (massique) = + Cp(T3 -T2r)
= 1.004 (1050 + 273 - 814.33) = 511.2 ≈ 511 kJ/kg
ηré = Wré-NET (massique)/Qc (massique) = 148/511 = 0.29
ηré = 29 %
On peur remarquer que:
ηré < ηth
