1. Fourier's Law: Conduction
1.1. Definitions
We have seen that this difference ΔT12 betwenn two points respectively a temperature T2
and T2 can be expressed by the Fourier's law which states that the flow ?J(the thermal energy
that passes per unit time) through the surface A of a cube across the length d is :br>
ΔJ = K (T1 - T2)A/d; where K is the thermal conductivity of the cube. Let's write:
ΔJ = K (T1 - T2)A/d = Q = κ A T12; where: κ = K/d.
- K is the thermal conductivity,
- κ is the conductance,
- Q the heat flux, and
- R = d/KA is the thermal resistance .
Thus:
Q = (K A /d)ΔT12 = κ A ΔT12 = (1/R) ΔT12
Q = ΔT12/R
where R = d/KA
Q in Watt (W), ΔT12 in oC or oK, R in oC/W, and
K in W/oC . m
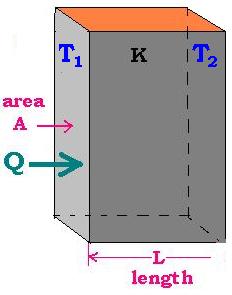
1.2 Application 1: Fourier's Law for a wall
1.2.1. One wall
|
For this case here, the surface at left is A and d = L. Let's write:
R = L/KA and
Q = K A ΔT12/L
We have an analogy with electrical circuis, where Q is the electrical current I,
&Delata;T is analog to the potential electrical difference, and the electrical resistance
is equivalent to the thermal resistance. As with electrical connections in series, we add
the thermal resistances Σri.
|
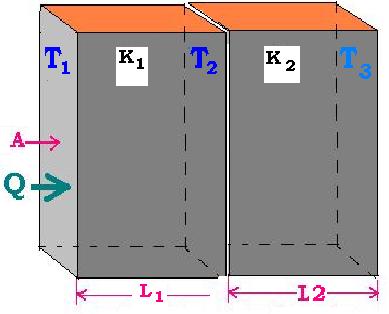
1.2.2. Two or more walls
If another wall, with K2 as the thermal conductivity coefficient, is juxtaposed with
the first, we write:
Rtotal = R1st + R2nd = (1/A) [L1/K1 + L2/K2]
and :
Q = ΔT13/Rtotal
Because T13 = T12 + T23 = (T1 - T2 )+ (T2 - T3)
For more than two walls, we have:
Rtotal = Σ Ri
= (1/A) Σ[Li/Ki]
and
Q = ΔTinitial-final/Rtotal
|
|
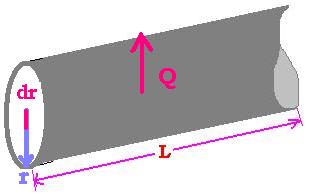
1.3. Application 2: Fourier's Law for a tube
|
|
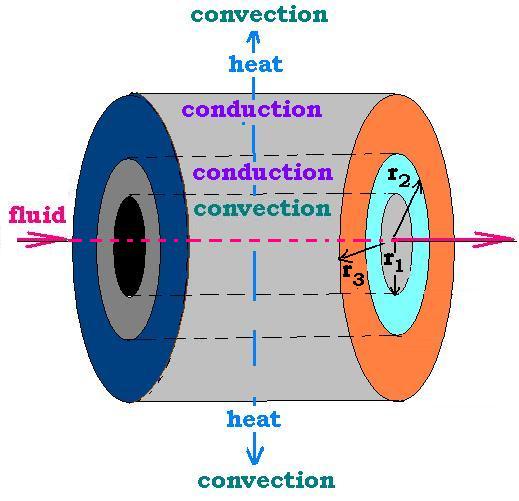
Let's consider a tube full of material of thermal conductivity K. In this case the heat flux is
directed laterally across the surface S = 2πrL. The thermal resistance is equal to R. R varies.
How to calculate R?
|
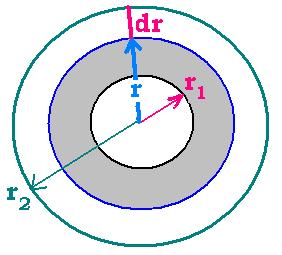
1.4. Thermal resistance formula
|
If dr is the differential resistance, we can write:
dR = dr/KA = dr/K 2πrL = (1/K 2πL)dr/r → R
= (1/K 2πL) ∫rd/r = (1/K 2πL) Ln (r)[r1 → r2]
R = [Ln (r2/r1)]/K 2πL
|
|
2. Fourier's Law: Convection
In the case of convection, we take the thermal conductivity for the conduction
is replaced by the thermal convection h. The related thermal resistance is given by:
R = 1/hA
A is the surface where the convection occurs from.
|
3. Conduction & Convection
|
The rule is to add the thermal resistances to obtain the total
thermal resistance Rtotal = Σ Rconduction + Rconvection
In the case of walls:
Rtotal = (1/A) Σ(Li /Ki)
In the case of tubes:
Rtotal = Σ [Ln(ri+1/ri)/2πKiLi]
In the general case, we have:
Rtotal = (1/A) Σ(Li /Ki)
+ (1/A)Σ(1/hi)
|
|
4. Heat exchanger:
4. 1. Differential Temperature Logarithm Mean: DTLM
We have Q = ΔT/R where the thermal resistance is equal to R for a static system; where there
is no current of fluid. In the case in which we have a heat exchanger of two currents: 1 cold current
and 1 hot current that will heat the colder; we express the heat flux Q as:
Q = U A ΔTm
where K/L is replaced by U.
U is called the global heat exchange coefficient and ΔTm the differential
temperature logarithm Mean (DTLM).
What's the expression of the DTLM?
In the expression Q = U A ΔT, Q and U are constant; but A and Δ vary. Let's write the
expression as follows:
(Q /U ) [1/ΔT]= A and calculate the mean of the two side of this expression, we have:
(Q /U ) <(1/ΔT)>= <A>
(Q /U ) [1/(ΔT1 - ΔT2)] ∫(dΔT/ΔT)= (1/A) ∫ A dA
[ΔT: ΔT1 → ΔT2]
(1/A) ∫ A dA = A and
<(1/ΔT)>= [1/(ΔT1 - ΔT2)] ∫(dΔT/ΔT)
= [1/(ΔT1 - ΔT2)] Ln (ΔT)=
[(Ln (ΔT1/ΔT2))/(ΔT1 - Δ2)]
We find:
ΔTm = [ΔT1 - ΔT2]/[Ln (ΔT1/ΔT2]
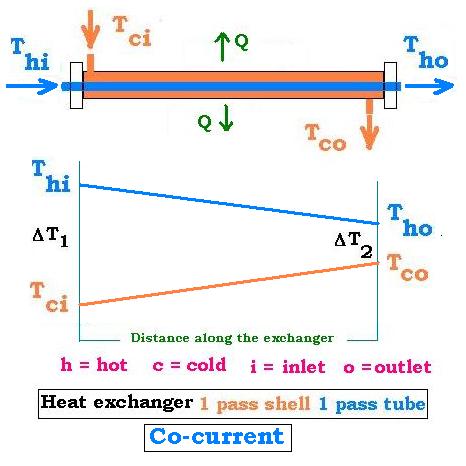
4.2. Co-Current: 1 shell pass & 1 tube pass
|
The system is counter-current; that is the directions of the two currents are the same.
ΔT1 = Thi - Tci
ΔT2 = Tho - Tco
ΔTm = [ΔT1 - ΔT2]/[Ln(ΔT1/ΔT2)]
|
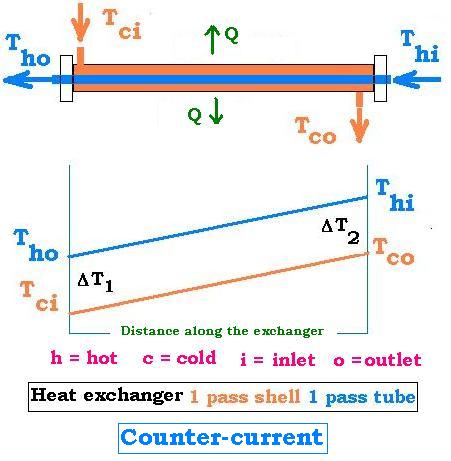
4.3. Counter-Current: 1 shell pass & 1 tube pass
The system is counter-current; that is the directions of the two currents are opposite.
ΔT1 = Tho - Tci
ΔT2 = Thi - Tco
ΔTmcc = [ΔT1 - ΔT2]/[Ln(ΔT1/ΔT2)]
|
|
4.4. Multipasses shell and tube
In this case, We define the DTLM as follows:
DTLM = F (ΔTm)cc.
F is a correction factor defined as the value of
a R-function of P, that is FP(P); geven by charts.
Here are the four steps:
1. calculate:ΔTmcc
(counter current 1 pass shell and 1 pass tube)
2.
Calculate the two defined ratios P and R as follows:
P = ΔT(tube)/ΔT(in-in)
and
R = ΔT(shell)/ΔT(tube)
Where:
ΔT(tube) = |T(tube-in) - T(tube-out)|
ΔT(shell) = |T(shell-in) - T(shell-out)|
ΔT(in-in) = |T(tube-in) - T(shell-in)| (or the maximum temperature difference)
Expressed in absolute values.
3. find the factor F in the charts.
4.Calculate the related DTLM
DTLM = F (ΔTm)cc.
F is a correction factor defined as the value of
a R-function of P, that is FP(P); geven by charts.
|
Example :
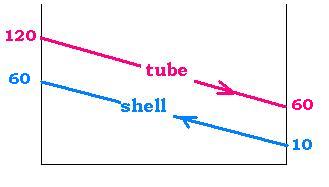
|
1-2 Heat Exchager ( 1 pass shell and 2 passes tube)that cools water going through tubes
ΔT(tube) = T(tube-in) - T(tube-out) = 120 - 60 = 60 oC
ΔT(shell) = T(shell-out) - T(shell-in) = 60 - 10 = 50 oC
ΔT(in-in) = T(tube-in) - T(shell-in)
= 120 - 10 = 110oC
Then:
ΔT1 = 120 - 60 = 60
ΔT2 = 60 - 10 = 50
ΔTmcc = (60 - 50)/Ln(60/50) = 55.0
P = ΔT(tube)/ΔT(in-in) = 60/110 = 0.55
R = ΔT(shell)/ΔT(tube) = 50/60 = 0.83
The chart gives: F = 0.95
ΔTm = F. ΔTmcc
= 0.95 x 55.0 = 52.25 oC.
|
4.5. Energy conservation
|
The shell:
Let's assume a fluid of thermal convection h circulate from the left to the right across a shell. Its rate D
is the quantity of fluid, per unit time, crossing the surface S1 = π r12.
At the entrance, the fluid has a temperature Thi and at the exit, it becomes less hot and has a
temperature Tco (Thi > Tco). If the specific heat at constant volume
of the fluid is cv, and the its mass is m contained in the part volume V = S1 L; then
the energy loss of this fluid is: m cv ΔTfluid-shell ; where ΔThc = Thi - Tco
is the temperature difference.
This difference in temperature occurs when the fluid touches the wall of the tube of thermal
conductivity kfluid-tube and heated it.
The tube:
If the temperature of the fluid passes from Tci inside the
tube, that is before crossing the tube and Tho the temperature outside the tube, the
difference ΔTfluid-tube = Tci - Tho.
Energy conservation
The loss of energy for the fluid in the shell is retreived by the fluid in the shell; that is
Qfluid-tube = Qfluid-shell or
mfluid-tube cfluid-tube ΔTfluid-tube = mfluid-shell cfluid-shell ΔTfluid-shell
As the rate D = dm/dt; we have:
[D c ΔT]fluid-tube = [D c ΔT]fluids-hell = U A ΔTm
|
|