Physique
Chimie
Électricité
Mathématiques
Calculateurs Scientifiques
© The scientific sentence. 2010

| |
|
Articles
Science and societies
Parallèles , vecteurs et parallélogrammes
Loi des sinus, loi des cosinus
Cercle inscrit et circonscrit au triangle
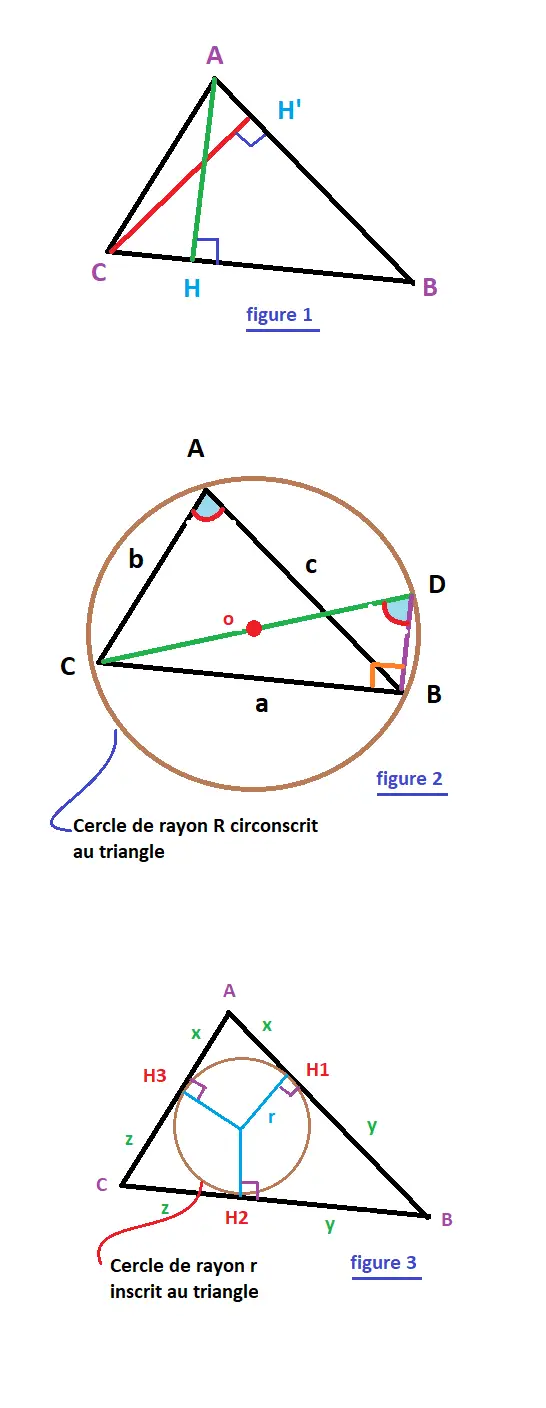
1) Loi des sinus dans le triangle ABC (figure 1):
sin (B) = AH/c , sin (C) = AH/b → AH = c sin (B) = b sin (C)
→ sin (B)/b = sin (C)/c (a)
De même,
sin (B) = AH'/a , sin (A) AH'/b → AH' = a sin (B) = b sin (A)
→ sin (B)/b = sin (A)/a (b)
(a) et (b) →
sin (A)/a = sin (B)/b = sin (C)/c (1)
C'est la loi des sinus .
2) Aire du triangle (figure 1):
S = Aire(ABC) = a x AH/2 = a b sin (C) /2 = a c sin (B) /2
= c AH' /2 = a c sin (B) /2 = b c sin (A) /2
→ S = a b sin (C) /2 = a c sin (B) /2 = b c sin (A) /2
→ 2S = a b sin (C) = a c sin (B) = b c sin (A)
→
2S /abc = sin (A)/a = sin (B)/b = sin (C)/c (2)
3) Aire du triangle ABC , et rayon du cercle circonscrit (figure 2):
Nous avons : mes (A) = mes (D) : Ce sont deux angles
qui interceptent le même arc (BC)
L'angle B est droit, puisque le point B est sur
le cercle et le côté CD est le diamètre du
cercl,
CD = 2R
Il vient :
sin (D) = sin (A) = a/CD = a/2R. D'où:
sin (A)/a = 1/2R
D'après la relation (1)
sin (A)/a = sin (B)/b = sin (C)/c = 1/2R
D'après la relation (2) 2S/ abc = 1/2R . D'où:
4RS = abc (3)
4) Aire du triangle ABC, rayon de son cercle inscrit r , et son
demi-périmètre P (figure 3):
Le dmi-périmètre du triangle ABC est:
P = 1/2( a + b + c)
Nous avons:
AH1 = AH3 = x d'après la propriété de Pythagore
De meme : BH1 = BH2 = y et CH2 = CH3 = z
On a:
S = Aire du triangle (ABC) = 2(rx/2 + ry/2 + rz/2) =
r(2x + 2y + 2z)/2 = r (a + b + c)/2 = rP
D'où:
S = rP (4)
(3) et (4) → abc = 4RS = 4RrP
abc = 4Rr(a + b + c)/2 = 4Rr(a + b + c)/2 = 2Rr(a + b + c) , ou
(a + b + c)/abc = 1/2Rr (5)
-- Abdurrazzak Ajaja
fevrier 2023
|
|