Articles
Science et sociétés
Mathématiques, variation des fonctions

Exercice 1:

Soit la fonction f définie par :
f(x) = 5x² + 6 x + 15

a) Pour tout x > 0, nous avons:

x > 0 → 6x > 0 → 6x + 15 > 0
→ 5x² + 6 x + 15 > 5x²
C'est à dire :

f(x) > 5x²

b) On cherche un β > 0 tel que :
Pour tout x > β, on ait f(x) > 5 x 10³⁰

Ce β répond à la question:

5 x β² = 5 x (10¹⁵)². D'où: β = 10¹⁵

β = 10¹⁵


Exercice 2:

On considère la fonction g définie par :
g(x) = x/(1 + x²)

1) Parité de la fonction g :

g(- x) = - x/(1 + (-x)²) = - x/(1 + x²) = - g(x)

g(x) = - g(x), la fonction est impaire

La courbe (Cg) de la fonction g alors est symétrique par rapport à l’origine du repère.

2) g(u) - g(v) = u/(1 + u²) - v/(1 + v²)
= [u(1 + v²) - v(1 + u²) ] /(1 + u²)(1 + v²)
= [u + uv²) - v - vu²) ] /(1 + u²)(1 + v²)
= [u - v + uv²)- vu²) ] /(1 + u²)(1 + v²)
= [u - v + uv(v - u) ] /(1 + u²)(1 + v²)
= (u - v)(1 - uv)/(1 + u²)(1 + v²)

En simplifiant par (u - v), on obtient:
(g(u) - g(v))/(u - v) =
(1 - uv)/(1 + u²)(1 + v²)

Taux de variation = (g(u) - g(v))/(u - v) =
(1 - uv)/(1 + u²)(1 + v²)

3) (1 + u²) et (1 + v²) sont positifs, donc le signe du Taux est celui simplement du facteur (1 - uv)

• Taux > 0 si (1 - uv) > 0 → uv < 1
• Taux < 0 si (1 - uv) < 0 → uv > 1

a) Sur l'intervalle [0,1], signe du Taux = signe de (1 - 0x1)= sing de (1) . Il est positif. La fontion est croissante.

Sur l'intervalle [0,1], la fontion est croissante.

b) Sur l'intervalle [1, +∞[ , signe du Taux = signe de (1 - 1x∞)= sing de -&infin . Il est négatif. La fontion est décroissante.

Sur l'intervalle [1, +∞[ , la fontion est décroissante.

4) La fonction g est impaire. Sa courbe (Cg) est symétrique par rapport à l’origine du repère. Ainsi, sur le domaine symétrique, R^- :

• Sur l'intervalle [-1,0], la fontion reste croissante.
• Sur l'intervalle ]-∞, -1] , la fontion est décroissante.

5)


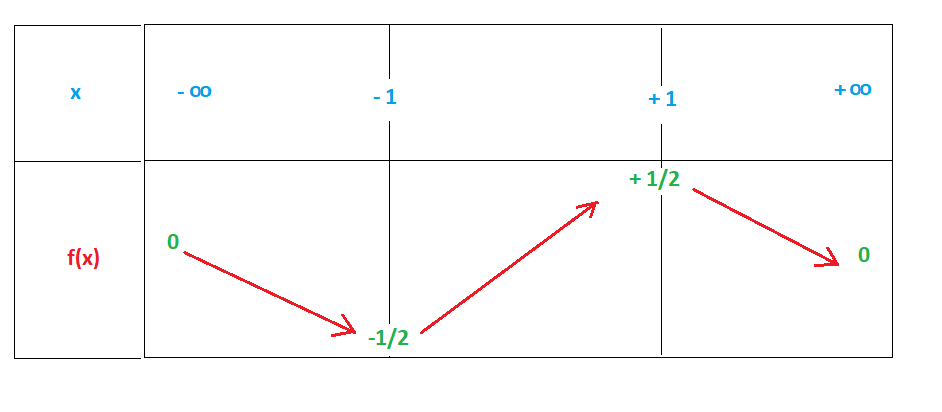
6)Extrémités de la fonction g:

• en - ∞ g(x)= x/(1 + x²) s'approche de x/( x²) = 1/x et tend vers zéro
• en x = -1, g(-1) = -1/(1 + (-1)²) = -1/2
• en x = +1, g(+1) = - g(-1) = +1/2
• en + ∞ g(x)= x/(1 + x²) s'approche de x/( x²) = 1/x et tend vers zéro


Exercice 3:

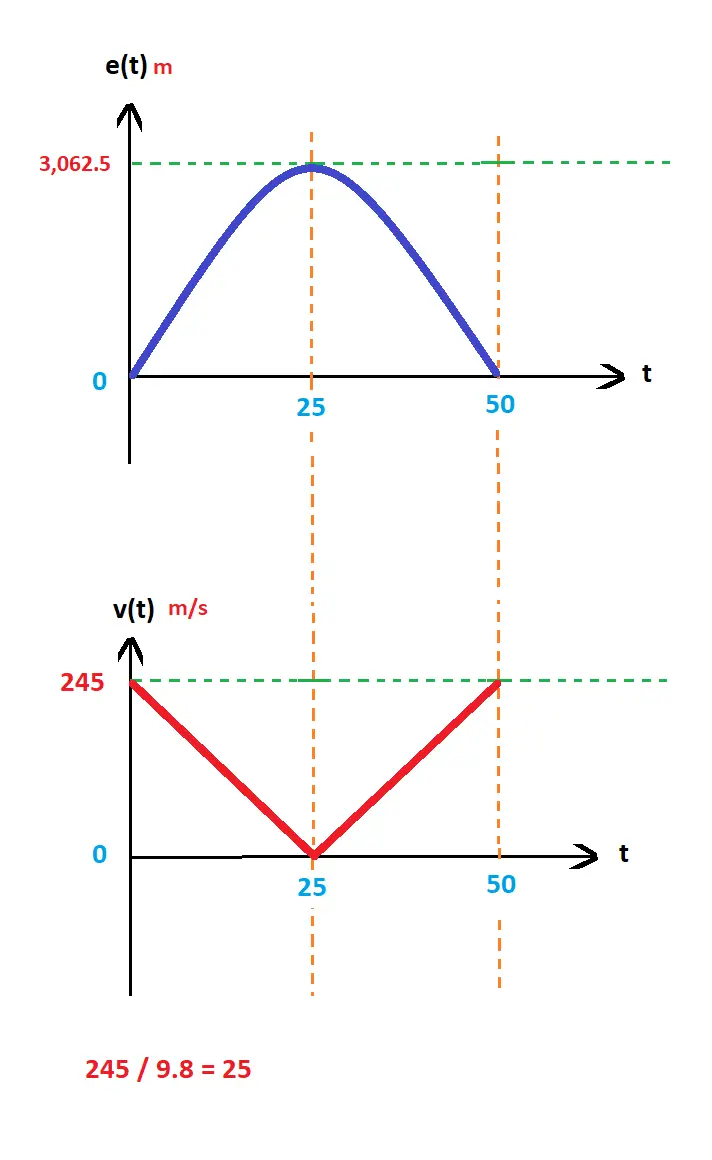
1) Projectile d'équation du mouvement: e(t) = 245 t - (9.8/2) t²
. L'équation de vitesse est v(t) = 245 - 9.8 t

2) a) Au point culminant, la vitesse du projectile est nulle , donc:
245 - 9.8 t = 0 → t = 245/9.8 = 25 secondes.

t_c = 25 secondes.

b) Le projectile passe au point de départ quant e(t) = 0. Cest à dire :

245 t - (9.8/2) t² = 0 → 245 - (9.8/2) t = 0 →
245 = (9.8/2) t → t = 2 t_c = 2 x 25 = 50 secondes

t_d = 50 secondes.

c) La hauteur du point culminant est e(25)

e(25) = 245 x 25 - (9.8/2) (25)² = 6,125 - 3,062.5= 3,062.5 m soit environ 3 km

e_c = 3 km

c) La vitesse du projectile au point culminant est nulle .

v_c = 0 m/s

d) La vitesse du projectile au retour du point de départ est v(50).

v(50) = 245 - 9.8 x 50 = 245 - 490 = - 245
= 245 m/s , vers le bas.

v_d = 245 m/s

-- Abdurrazzak Ajaja
mars 2023