Dirac delta function

1. The general definition

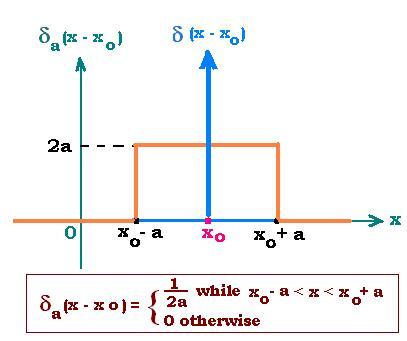
The general definition of this function is:
δ_a (x - x_o) = 1/2a in [x_o - a , x_o + a] and zero otherwise.
δ (x - x_o) = lim δ_a (x - x_o) a → 0
∫ f(x) δ(x - x_o) dx = ∫ f(x) lim δ_a(x - x_o) dx a → 0 [- ∞, + ∞]
= lim ∫ f(x) δ_a(x - x_o) dx a → 0 [- ∞, + ∞]
= lim ∫ f(x) δ_a(x - x_o) dx a → 0 [x_o - a, x_o + a]
The variable x is now taken in the interval [x_o - a, x_o + a], then if a → 0 then x → x_o. Therefore:
∫ f(x) δ(x - x_o) dx = lim (1/2a) ∫ f(x_o) dx = f(x_o lim (1/2a) ∫ ) dx = f(x_o) lim (1/2a) [x] (between x_o - a and x_o + a) a → 0
= f(x_o) lim (1/2a) [(x_o + a) - (x_o - a)] = f(x_o) lim (1/2a) [2a] = f(x_o). Therefore:

∫ f(x) δ(x - x_o) dx = f(x_o)

At the origin: x_o = 0, we have the δ function &delta(x) such as:
∫ f(x) δ(x) dx = f(0).

2. Properties of the Dirac function