A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Electromagnetic equations revisited
1. Maxwell equations
The Maxwell's equations in their differential forms related to the free space are:
- ∇ . E = ρ/ε0 = 0 (1)
- ∇ x E = - ∂B/∂t (2)
- ∇ . B = 0 (3)
- ∇ x B = μ0 (J + ε0 ∂E/∂t)
= μ0 ε0 ∂E/∂t (4)
2. ∇ x∇ xA = ?
Let's take the curl of the vector A (Ax,Ay,Az):
∇ x A =
( ∂Az/∂y - ∂Ay/∂z, ∂Ax/∂z -
∂Az/∂x, ∂Ay/∂x - ∂Ax/∂y)
Now let's take the curl of its curl:
∇ x ∇ x A = (Component-1, Component-2, Component-3)
Component-1 = ∂(∂Ay/∂x - ∂Ax/∂y)∂y - ∂(∂Ax/∂z - ∂Az/∂x)∂z
Component-2 = ∂(∂Az/∂y - ∂Ay/∂z)∂z - ∂(∂Ay/∂x - ∂Ax/∂y)∂x
Component-3 = ∂(∂Ax/∂z - ∂Az/∂x)∂x - ∂(∂Az/∂y - ∂Ay/∂z)∂y
That is :
Component-1 = ∂2Ay/∂x∂y - ∂2Ax/∂y2 - ∂2Ax/∂z2 + ∂2Az/∂x∂z
Component-2 = ∂2Az/∂y∂z - ∂2Ay/∂z2 - ∂2Ay/∂x2 + ∂2Ax/∂y∂x
Component-3 = ∂2Ax/∂z∂x - ∂2Az/∂x2 ∂2Az/∂y2 + ∂2Ay/∂z∂y
Adding and subtracting:
∂2Ax/∂x2, ∂2Ay/∂y2, and ∂2Az/∂z2 in the first, second and third components of the vector A
respectively, we get:
Component-1 = ∂2Ay/∂x∂y - ∂2Ax/∂y2 - ∂2Ax/∂z2 + ∂2Az/∂x∂z + ∂2Ax/∂x2 - ∂2Ax/∂x2
Component-2 = ∂2Az/∂y∂z - ∂2Ay/∂z2 - ∂2Ay/∂x2 + ∂2Ax/∂y∂x + ∂2Ay/∂y2 - ∂2Ay/∂y2
Component-3 = ∂2Ax/∂z∂x - ∂2Az/∂x2 - ∂2Az/∂y2 + ∂2Ay/∂z∂y + ∂2Az/∂z2 - ∂2Az/∂z2
Hence:
Component-1 = ∂(∇ . A)∂x - ∇ . (∇ Ax)
Component-2 = ∂(∇ . A)∂y - ∇ . (∇ Ay)
Component-3 = ∂(∇ . A)∂z - ∇ . (∇ Az)
That is the scalar:
∇ (∇ . A) - ∇ . (∇ A)
∇ x∇ xA = ∇ (∇ .A) - (∇ .∇ A) (5)
Since ∇ .∇ = ∇ 2 = Δ , that is the Laplacian operator, we have:
∇ x∇ xA = ∇ (∇ .A) - ΔA (6)
3. The two electromagnetic equations
∇ x ∇ x E = - ∂/∂(∇ x B) = - μ0 ε0 ∂2E/∂t2
Since ∇ .E = 0, it remains, according to the relationship (6): - Δ E = - μ0 ε0 ∂2E/∂t2
That is:
Δ E - μ0 ε0 ∂2E/∂t2 = 0. Or:
Δ E - (1/c2) ∂2E/∂t2 = 0
(7)
with:
c = 1/[μ0 ε0]1/2.
c = 3.00 x 108 m/s, the speed of light in the vacuum.
Now, let's take the curl of the curl of B, we have:
∇ x ∇ x B = μ0 ε0 ∂ (∇ x E) /∂t, according to the
relationship (4). According to the relationship (3), we have then:
∂ (∇ x E) /∂t = - ∂2 B /∂t2. From the relationship (6), we
have then:
∇ x ∇ x B = - Δ B = - μ0 ε0 ∂2 B /∂t2
Or:
Δ B - (1/c2) ∂2B /∂t2 = 0
(8)
4. Example: simple case
We will show that the plane waves are the solutions for the Maxwell's equations:
Let's take the simple case where E = Ex = Ex0 cos(ωt - kz),
Ey = 0 and Ez = 0. We have:
∇ x E = (0, ∂Ex/∂z,0) = k Ex0 sin(ωt - kz) (in the y direction)
Using the equation (2), we have:
∇ x E =
k Ex0 sin(ωt - kz) = - ∂B/∂t. We integrate to obtain:
B = (k/ω) Ex0 cos(ωt - kz)
Since: ω/k = c, then:
B = (Ex0/c) cos(ωt - kz) (in the y direction)
Therefore:
if:
E(z,t) = Ex = Ex0 cos(ωt - kz) (in the x direction)
Then:
B(z,t) = (Ex0/c) cos(ωt - kz) (in the y direction)
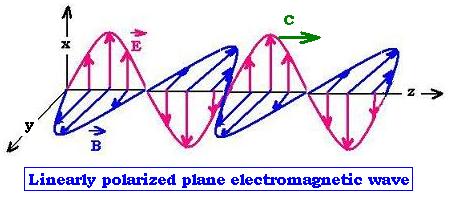
The above expression of E(z,t) and B(z,t) are solutions of the Maxwell equations. E(-z,t) and B(-z,t)
are also solutions of these equations. Therefore, all the linear combination of these expressions:
E(z,t) = ∑ [αiE(z,t) + βi E(-z,t)]
B(z,t) = ∑ [αiB(z,t) + βi B(-z,t)]
are also solutions.
©: The scientificsentence.net. 2007.
|
|
|