Green's function

Helmholtz's, Poisson's equations and the like are not obviously solved. Dealing with potentials, maily in Electromagnetic field, solving such equations, requires an understanding and the use of the Green's Function. The G'sF is a technique generally used to solve linear differential equations in the presence of a source . In this lecture, we will use the Dirac Delta function, the Fourier Transform to set the solutions of a PDE (Partial Differential Equation). We will set a general form for the solution of the equation of diffusion, and consider the case of the Helmholtz's equation in three dimensions with a second member not null.

1. Expression of the Green's function

The equation of diffusion has the form:
(Δ + k²) ψ_k(r) = U(r) ψ_k(r)     (1)
Δ is the Laplacien, U(r) is the potential enegy and k is a parameter. The operator Δ + k² is called the kernel, and
S(r) = U(r) ψ_k(r)     (3)
is called the source.

Now, let's write:
(Δ + k²) G_k(r) = δ(r)     (4)
δ(r) is the Dirac's function. It can be written as δ⁽³⁾(r) = δ(x)δ(y)δ(z)

The solution needed for the equation (1) is:
ψ_k(r) = ψ_0,k(r) + ∫ G_k(r - r') S(r') dr'    (5)
Where ψ_0,k(r) is the solution for the homogenous equation, that is for S(r) = 0.
In this case the equation (1) becomes: (Δ + k²) ψ_0,k(r) = 0. This stationary state is of the form:
ψ_0,k(r) = e^ik.r     (5')
To verify that ψ_k(r) is really the solution for the equation (1), apply the operator Δ + k² to it ( to the equation (5)) to find:
(Δ + k²)ψ_k(r)= (Δ + k²)ψ_0,k(r) + ∫ (Δ + k²) G_k(r - r') S(r') dr' = 0 + ∫δ(r-r')S(r')dr'= S(r) .
dr' = d³(r')

2. Solutions of the Green's function for a PDE

Let's consider the example mentionned above and solve the equation (4).
First, write the Fourier Transform G^FT(q) of the green function G(r).
G_k^FT(q) = (1/(2π)³)∫G_k(r)e^-iq.r dr     (6)
With:
G_k(r) = ∫ G_k^FT(q) e^+iq.r dq     (7)
For the delta function, according to ∫ f(x) δ(x-a) dx = f(a), we have:
δ^FT(q) = (1/(2π)³)∫δ(r)e^{- iq.r} dr = (1/(2π)³)e^{- iq.0} = 1/(2π)³

Let's write: δ^FT(q) = 1/(2π)³    (8)
Then:
δ(r) = (1/(2π)³)∫ e^+iq.r dq     (9)

Applying the kernel to the equality (7) yields:
(Δ + k²) G_k(r) = ∫(Δ + k²) G_k^FT(q) e^+iq.r dq = ∫(- q ² + k²) G_k^FT(q) e^+iq.r dq     (10)
According to (4), we can equate (9) and (10): (- q ² + k²) G_k^FT(q) = 1/(2π)³
Or: G_k^FT(q) = - 1/(2π)³/(q ² - k²)    (11)
The relation (7) becomes:

G_k(r) = (- 1/(2π)³) ∫ (e^+iq.r /(q ² - k²)) dq     (12)

3. Integrated expresson of the Green's function for a PDE

We will use the following figure to integrate the relation above:

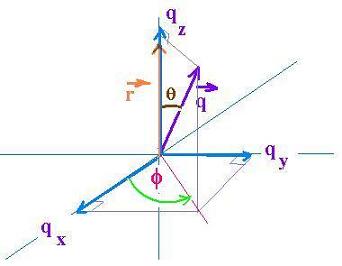
The spherical coordinates of the vector q are: q, θ, and φ. Therefore, the integral element is q²dq sinθ dθ dφ. φ from 0 to 2π, θ from 0 to π and q from 0 to ∞
We have chosen r parallel to k_z, We have:
q.r = qr cosθ. Since ∫ dφ = 2π Then, the relation (12) becomes:
G_k(r) = (- 1/(2π) ²) ∫ ∫ sinθ dθ (e^+iq.rcosθ /(q ² - k²)) q² dq     (13)
= (- 1/(2π)²) ∫ (q²/(k² - q ²)) dq ∫ d(- cosθ)(e^+iq.rcosθ )
(cosθ from +1 to -1 and q from 0 to ∞)
= (- 1/(2π)²) ∫ (e^+iq.r - e^-iq.r) (q²/(q ² - k²)) dq (1/iqr)
= (- 1/(2π)²/ir) ∫(e^+iq.r - e^-iq.r)(q/(q ² - k²)) dq
= (- 1/(2π)²/ir)( ∫(e^+iq.r (q/(q ² - k²)) dq - ∫(e^-iq.r (q/(q ² - k²)) dq)     (14)
Let's change -q into +q in the second term. It becomes then as the first, except the integrale varies from - ∞ to 0 for this second term. The sum becomes the first term integrated from -∞ to +∞. We have then:

G_k(r) = (- 1/(2π)²/ir) ∫ (e^+iq.r (q/(q ² - k²)) dq)     (15)


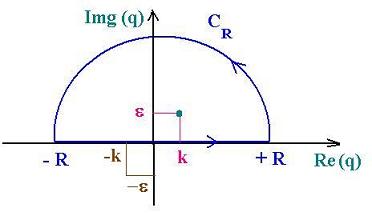
Now, we will integrate in the complex q plane. The following figure shows two contours (-R,+R) and C_R. Let's write:
∫_contourG_k(r) = ∫_{(- R,+ R)} G_k(r) + ∫_CR G_k(r)     (16)

We have: q ² - k² = (q - k) (q + k). Then two poles q = - k and q = + k.
In order to apply the residue theorem, we can write these two poles:
q_- = lim_{ε = 0} - k - iε and
q₊ = lim_{ε = 0} + k + iε

It follows that: ∫_contour e^+iq.r (q/(q + q_-)(q + q₊) dq = ∫ _{(- R, + R)}(e^+iq.r (q/(q - q₊)(q + q₊)) dq + ∫_CR(e^+iq.r (q/(q - q₊)(q + q₊)) dq     (17)

According to the Jordan's lemma, the above second term is null: ∫_CR(e^+iq.r (q/(q - q₊)(q + q₊)) dq = 0
Then:
∫_contour e^+iq.r (q/(q + q_-)(q + q₊) dq = ∫_{(- R,+ R)}(e^+iq.r (q/(q - q₊)(q + q₊)) dq     (18)
The pole q_- is outside the contour, then it will not contribute to the residue theorem.

Let's tend R towards ∞ and apply the residue theorem, then:
∫_contour e^+iq.r (q/(q ² - k²) dq = 2iπΣ(Residues inside the closed contour) = Residue (q₊)
Then: ∫_contour e^+iq.r (q/(q ² - k²) dq = 2iπResidue (q₊)
∫_{(-∞, + ∞)}(e^+iq.r (q/(q² - k²)) dq = 2iπ Residue (q₊) = 2iπ (q - q₊) e^+iq.r q/(q - q₊)(q + q₊) (for q = q₊) = 2iπ e^+i(q₊).r (q₊/(q₊ + q₊)
= 2iπ e^+i(q₊).r (q₊)/(2q₊) = lim (ε = 0) 2iπ e^{+i(k + iε).r}/2 = iπe^+i(k).r
The relationship (15) becomes:
G_k(r) = (- 1/(2π)²/ir) iπ e^{+i(k + iε).r} , or:

G_k(r) = - (1/4π) e^ikr /r     (19)

The relation (5) becomes;
ψ_k(r) = ψ_0,k(r) -1/4π∫ e^ik|r-r'|/|r-r'| U(r')ψ_k(r') dr'    (20)

From the relationships (5') and (19), the general solution of the equation (1) is:

ψ_k(r) = e^ik.r -1/4π∫e^ik|r-r'|/|r-r'| U(r')ψ_k(r') dr'     (21)


Remark:
The equation (19) is obtained with ε > 0. It's the outgoing solutioni, and written as:
G_k⁽⁺⁾(r)= (-1/4π) e^ikr /r    (22)
In the opposite contour (negative region) ε < 0 is considered, so the negative pole contributes. The other second solution is the incoming solution :
G_k^(-)(r)= (-1/4π) e^-ikr /r    (23)

4. Particular case

The solution for the main equation (1), with S(r) = 0 is the relationship (5'), that is:
ψ_0,k(r) = e^ik.r    (24)
But this solution is not unique. In fact the complete solution for this homogenous equation ((S(r) = 0) is:
ψ_0,k(r) = C e^ik.r    (25)
Where C is a constant.
In the case of k = 0, the main equation (1) becomes: Δ ψ₀(r) = U(r) ψ₀(r),
or: Δ ψ(r) = U(r) ψ(r)    (26)
The related particular solution is given by the relationship (21)
ψ₀(r) = C - 1/4π∫ 1/|r-r'| U(r') ψ₀(r') dr'     (27)
The particular case used for the magnetic and electric potentials is to set ψ (r) → 0 at infinity.
Therefore: C = 0. The equation:
Δ ψ(r) = S(r)    (28)
has then the solution:
ψ₀(r) = - 1/4π ∫ S(r') /|r-r'| d³(r')    (29)