Harmonic wave

The concept of pulse was introduced to get the features of a wave. the more interesting situation is that when the disturbance lasts in time in order to get energy transported by a wave itself from a point to another. The useful and simple disturbance wave function is a kind of sine function. Wiggling an object periodically in time constitutes an harmonic oscillator. Thus this particular disturbance can be conveyed in a medium to generate an harmonic wave.


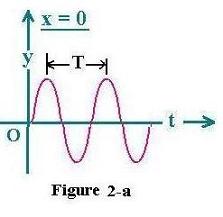
A harmonic oscillation, at certain point (x = 0) is written as:
y(t) = y(x = 0, t)= A sin(ωt);      (1)
where ω is the angular frequency, t the time variable and A is the amplitude of the oscillation. It is plotted on the figure 2-a:

For a given time (t = 0), the related harmonic wave function is written as:

y(x, t = 0) = A sin[(2π/λ)x]      (2)


Where λ is the wavelength that is the repeated distance of the wave. It is represented in the figure 2-b; which shows a "snapshot" of the wave at the instant t = 0.




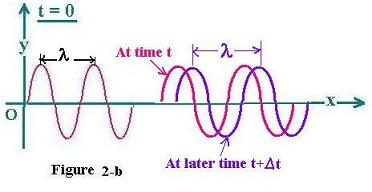
Since the shape of the function have to remain the same (wave function at x is equal the wave function at the time t before; that is at x - vt. Then the x-t dependance of the wave function is with x - vt
The equation (2) becomes:

y(x,t) = A sin[(2π/λ)(x - vt)]      (3)


The period T of oscillations is equal to the one of the wave.
We know that T = 2π/ω = 1/ν = λ/v. Where ν is the frequency of the wave. Introducing the wave number k = 2π/λ, the equation (4) can be written as:

y(x,t) = A sin(kx - ωt)      (4)

What's more, introducing the phase constant φ the equation (5) becomes:
y(x,t) = A sin(kx - ωt + φ)      (3.5)
Often we choose x = 0 at t = 0 such that φ = 0.

More details:
The angular frequency is the number of times, per unit time as a second, we complete a cycle, which is completed in the time T called period. In other word, It is the number of cycles we get per unit time.

As a moving particle over a circle, we can express the angular frequency by ω = dα/dt, where α is the angle, from the origin to the current point at the time t corresponding to the position of the moving particle. Integrating the former relation ∫dα = ∫ ω dt, we find 2π = ω T, so we have the expression of the period T = 2π/ω.

In the period T, we define a distance called the wavelength λ. It is the dispalacement of the disturbance (or the pulse) over the period of time T; hence λ = vT, where v is the speed of the pulse. Therefore v = λ/T = λ ω/2π. We define a new number called the wave number k = 2π/λ. Thus kv = ω. With x = vt, we have ωt = ωx/v = ω xT/λ = 2πx/λ = kx . Finally, the wave function becomes: y = f(x,t) = Asint[k(x - vt] = Asint[kx - ωt].