A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Interferometers
A divice used to study interferences is called interferometer, like
the Michelson and Fabry-Perot interferometers that we will study in this chapter.
1.Michelson interferometer
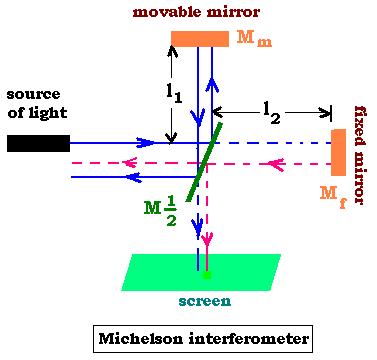
&psi:1(x,t) = A1 sin(ωt - kx)
ψ2(x,t) = A2 sin(ωt - kx + δ)
δ is the phase shifting between the two waves.
ψ(x,t) = &psi:1(x,t) + &psi:2(x,t)
I = |ψ(x,t)|2 = |ψ1(x,t)|2 + |ψ2(x,t)|2 +
2 ψ1(x,t) ψ2(x,t) = I1 + I2 + 2[I1I2]1/2
sin(ωt - kx) sin(ωt - kx + δ)
We can write the third term as:
I12 = 2[I1I2]1/2 sin(ωt - kx)sin(ωt - kx + δ)
With:
sin a sin b = [cos(a - b) - cos(a + b)]/2. Hence:
sin(ωt - kx) sin(ωt - kx + δ) = [cos(&delta) - cos(2ωt - 2kx + δ)]/2
The term cos(2ωt - 2kx + δ) oscillates. It does not contribute to the intensity. Then:
I12 = 2[I1I2]1/2 cos(δ)
We have, according to the geometry of the interferometer:
I1 = I2 = Io/4
Thus:
I = I1 + I2 + I12 =
I = Io/2 + 2(Io/4) cos(&delta) = Io/2 + (Io/2) cos(δ)
I = Io/2 (1 + cosδ)
The phase shifting δ = k(xo - x1) = (2π/λ)Δx
Hence: a measure of the intensity I and the distance between fringes Δx gives the
value of the wavelength λ
2. Fabri-Perot interferometer
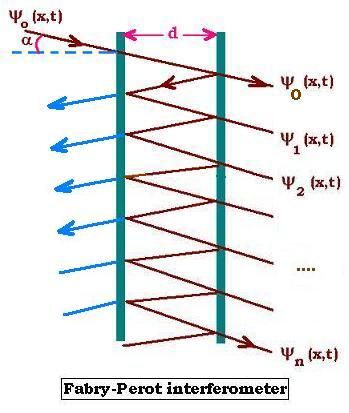
The phase shifting δ is δ = kd/cosα + d/cosα = 2 kd/cosα
ψ0(x,t) = A0 sin(ωt - kx)
ψ1(x,t) = A1 sin(ωt - kx + δ)
ψ2(x,t) = A2 sin(ωt - kx + 2δ)
ψ3(x,t) = A3 sin(ωt - kx + 3δ)
....
ψn(x,t) = An sin(ωt - kx + nδ)
ψ(x,t) = ∑ψj(x,t) [j: from 0 to n]
Let's work with the complex notation:
ψj(x,t) = Aj sin(ωt - kx + jδ) =
Aj exp {i(ωt - kx + jδ)}
= Aj exp {i(ωt - kx)} exp{ijδ)}
ψ(x,t) = ∑ Aj exp {i(ωt - kx)} exp{ijδ)} =
exp {i(ωt - kx)} ∑ Aj exp{ j iδ)}.
We have:
A0 = T Ao
A1 = R2 T Ao
A3 = R3 T Ao
---
An = Rn T Ao
With : T = 1 - R, we get:
An = (1 - R) Rn Ao
Then:
∑ Aj exp{ j iδ)} = (1 - R) Ao ∑ Rj exp{ j iδ)}
We have:
∑ Rj exp{ j iδ)} = ∑ [R exp{iδ}]j [j: from 0 to n (n+1 reflections)]
= (1 - Rn exp{inδ}) /(1 - R exp{iδ})
ψ(x,t) = exp {i(ωt - kx} (1 - R) Ao ∑ Rj exp{ j iδ)}
= exp {i(ωt - kx)} (1 - R) Ao (1 - Rn exp{inδ}) /(1 - R exp{iδ}).
(1 - Rn exp{inδ}) &asym; 1 because R< 1; hence:
ψ(x,t) = exp {i(ωt - kx)} (1 - R) Ao /(1 - R exp{iδ})
ψ(x,t) = Ao (1 - R) exp {i(ωt - kx )} /(1 - R exp{iδ})
I = |ψ(x,t)| = (1 - R)2 A2o |1/(1 - R exp{iδ})|
|1/(1 - R exp{iδ})| = 1/|(1 - R exp{iδ})| = 1/(1 - R exp{iδ})(1 - R exp{-iδ}) =
1/(1 - R exp{-iδ} - R exp{iδ + R2) = 1/(1 + R2 - 2R [exp{-iδ} + exp{iδ] /2)
exp{-iδ} + exp{iδ] /2 = cos δ = 1/(1 + R2 - 2Rcosδ)
I = |ψ(x,t)| = (1 - R)2A2o /(1 + R2 - 2Rcosδ)
With A2o = Io, we have:
I = (1 - R)2 Io /(1 + R2 - 2Rcosδ)
I = (1 - R)2 Io /(1 + R2 - 2Rcosδ)
1 + R2 - 2Rcosδ = 1 + 2R + R2 - 2R - 2Rcosδ =
= 1 - 2R + R2 + 2R - 2Rcosδ = (1 - R)2 + 2R(1 - cos δ)
With:
1 - cos δ = 2 sin2(δ/2), we have then:
I = (1 - R)2 Io /((1 - R)2 + 4R sin2(δ/2))
I = Io (1 - R)2 /((1 - R)2 + 4R sin2(δ/2))
I = Io (1 - R)2 /((1 - R)2 + 4R sin2(kd/cosα))
With α ≈ 0:
I = (1 - R)2 Io /((1 - R)2 + 4R sin2(kd))
Finally:
I = Io (1 - R)2 /((1 - R)2 + 4R sin2(2πd/λ))
©: The scientificsentence.net. 2007.
|
|
|