A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Single slit diffraction
Intensity distribution
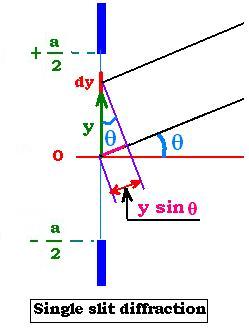
The slit of width "a" is divided into an infinite elementary slits "dy".
Each "dy" correspond to the elementary electric field dE. We will add
all these dE over the range [-a/2, +a/2] to find the resultant field E at
a point on the screen; then we square its amplitude to find its intensity
at this point.
If Ec, the amplitude of the electric field of the wave
emerging from the center of the slit, is uniformly distributed
along "y", we can write at y = y on the screen:
dE = Ec (dy/a) sin (ωt + φ). φ is the phase
difference between the wave from y = 0 and from y.
We have:
2π/φ = λ/y sin θ, thus: φ = (2 π/λ) y sin θ
Then: dy = dφ (λ/2 π sin θ), and
dE = Ec [ (λ/2 π sin θ)/a] sin (ωt + φ) dφ
Let's write:
β = π a sin θ/λ, thus:
dE = (Ec /2 β) sin (ωt + φ) dφ
If "y" varies from: -a/2 to +a/2, then φ varies from: - β to + β
We have then:
E = ∫ dE = ∫ (Ec/a) sin (ωt + φ) dy from -a/2 to +a/2
= ∫ (Ec /2 β) sin (ωt + φ) dφ from: - β to + β
We have the following trigonometric identity:
sin (ωt + φ) = sin ωt cos φ + cos ωt sin φ
Thus:
E = (Ec /2 β) [sin ωt ∫ cos φ dφ + cos ωt ∫ sin φ dφ] from: - β to + β
= (Ec /2 β) [sin ωt (sin φ) + cos ωt (- cos φ)] from: - β to + β
= (Ec /2 β) [sin ωt (2 sin β) + cos ωt (0)] = (Ec / β) sin β sin ωt
Thus:
I = (1/2)cεo E2 =
(1/2)cεo(Ec2) sin2 β / β2 =
Ic sin2 β / β2
With Ic = (1/2)cεo(Ec2)
Finally:
I = Ic sin2 β / β2
Ic = (1/2)cεo(Ec2),
β = (π a/λ) sin θ
©: The scientificsentence.net. 2007.
|
|
|