Wave packets

1. Superposition of two waves

Supperposing two waves in phase of equal frequency and amplitude just doubles the resultant amplitude; when they are out of phase, the two combined waves just cancel each other. Supperposing two waves in phase of equal frequency and different amplitudes just enlarge the resultant amplitude.
The most interesting is the supperposition of two or more waves of almost the same frequency that corresponds to the beats phenomenon.

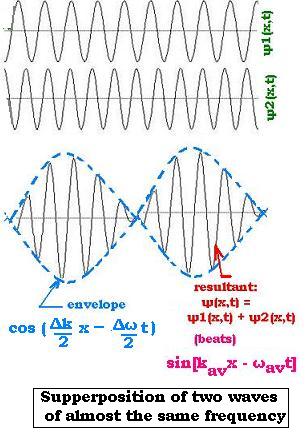
Let's consider the two following wave functions:
ψ₁(x,t) = A sin(k₁x - ω₁t)
ψ₂(x,t) = A sin(k₂x - ω₂t)

Which are waves traveling in the same direction with the same amplitude A, different wave number k and different angular frequency ω .

We use the principle of superposition to find the resultant wave ψ(x,t) = ψ₁(x,t) + ψ₂(x,t).
Then:
ψ(x,t) = A[sin(k₁x - ω₁t) + sin(k₂x - ω₂t)]

Using the trigonometric identity:
sin (a + b) + sin (a - b) = 2 sin a cos b;
With: a + b = x and a - b = y ,
we get: a = (x + y )/2 and b = (x - y)/2

Then:
sin (x) + sin (y) = 2 sin [(x + y )/2] cos [(x - y )/2]
It follows that:
ψ(x,t) = 2A sin ([k₁x - ω₁t + k₂x - ω₂t]/2) cos([k₁x - ω₁t - k₂x + ω₂t]]/2)
= 2A sin [(1/2)(k₁ + k₂)x - (1/2)(ω₁ + ω₂)t] cos[(1/2)(k₁ - k₂)x - (1/2)(ω₁ - ω₂)t]

Thus:
ψ(x,t) = 2A cos[(Δk/2)x - (Δω/2)t] sin[k_avx - ω_avt]     (1)

With:
Δk = k₁ - k₂
Δω = ω₁ - ω₂
k_av = (k₁ + k₂)/2
ω_av = (ω₁ + ω₂)/2

The factor cos[(Δk/2)x - (Δω/2)t] represents the envelope of the combined waves. The resultant wave expressed by the factor sin[k_avx - ω_avt] oscillates within the envelope with the wave number k_av and angular frequency ω_av. Each individual wave moves with its own phase volocity ω₁/k₁ and ω₂/k₂. The combined wave moves with the phase velocity ω_av/k_av. The envelope which represents the pulse or the wave packet moves at the group velocity Δω/Δk.

2. Superposition of many waves: The wave packet

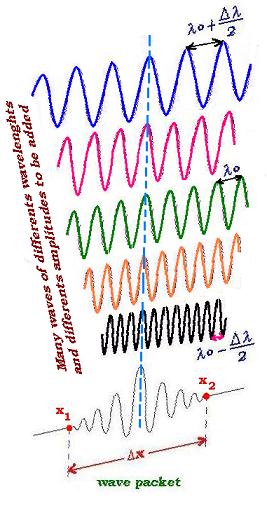
Combining many waves leads to a pulse or wave packet as for combining two waves. But the more we add waves the more the distance between the pulses becomes larger; and for a given time we can see less wave-packet pass through the direction of the propagation. In other words, a finite number of different monochromatic waves always produce infinite sequence of repeating pulses (wave groups). As we want to localize the packet, we need to stabilize the packet, we will then add an infinite number of waves with a particular well chosen amplitude. The effective idea is to fix a wave number k_o and let the envelope takes effect about this centred wave number k_o (or wavelength λ_o). The Gaussian is the appropriate example. It plays the role of having constructive interference over the space-time and destructive interference elsewhere.

The wave function of the wave-packet can then be written as:
ψ(x,t) = ∑ ψ_i(x,t) = ∑ A sin(k_ix - ω_it)
Or, with different amplitudes:
ψ(x,t) = ∑ A_i sin(k_ix - ω_it)     (2)

Wich is called Fourier series.

When dealing with a continuous spectrum, the Fourier series bocome the Fourier integral:
ψ(x,t) = ∫A(k) sin(kx - ωt) dk   (3)
k: - ∞ → + ∞

If Δx is the space where we can localize the packet-wave, |ψ(x,t)|²dx is the probability of finding the wave-packet within Δx. If Δk is the range around k_o that is set to form a wave packet, and Δx the region between the two consecutive points where the envelope is zero (Δx = x₂ - x₁); we can write from the relationship (1):
cos[(Δk/2)x₁ - (Δω/2)t] = 0; and cos[(Δk/2)x₂ - (Δω/2)t] = 0.

We can write: (Δk/2)x₁ - (Δω/2)t = π/2, and (Δk/2)x₁ - (Δω/2)t = 3π/2.
We have then:

(Δk/2)x₂ - (Δω/2)t - (Δk/2)x₁ + (Δω/2)t = π. That is: (Δk/2)(x₂ - x₁) = π, which is called:

The uncertainty principle: Δk Δx = 2π     (4)


Contrary to the Classical Mechanics that allows both the measure of the position and the momentum of a particle at a certain same time, Wave Mechanics allows just one, the other is uncertain. The above relation is set for the combination of two waves. It is not very precise. It tells us just in order to know precisely the position of the wave packet (or to localize a particle), then Δx small, we need a large range of wave numbers (Δk large). With ω = 2π ν, and k = 2π/λ = 2πν/v, and x = vt(ν is the frequency, v the velocity, and x the displacement of the particle), the above relation becomes Δω Δt = 2π. This relationship tells us also that to know precily (at a fixed small time) when the packet is located at a given point, we need a large range of frequencies ω. It has an important role in Electronis. It shows that the bandwidth must be large of a circuit to send a signal in a short time (a dial-up Internet connection works with a very narrow bandwidth about 50 Kbps (Kilo bits per second), whereas, a broadband connection can let move a large amount of data at about some Mbps (Mega bits per second).

3. Matter-wave concept

The de Broglie relationship set the wave-particle duality. Further, the description of matter particle by a wave packet is justifed by the fact they move at the same velocity. Indeed, the the wave-packet moves at the speed of the envelope called the group velocity v_g equal to Δω/Δk = dω/dk. This derivative is set about the most probable value of k that is k_o.

If a particle (relativistic) has the total energy E, E² = p²c² + m²c⁴, its mass m = m(v) = γm with γ = 1/[1 - v²/c²]^1/2, its impulsion p = γmv. With E = m(v)c² = γmc², we have E²v²/c² = p²c², then v = pc²/E.

But the derivative of the relationship E² = p²c² + m²c⁴ gives: 2EdE = 2c²pdp, that is pc²/E = dE/dP.
Using dE/dP = d(hω/2π)/d(hk/2π) = dω/dk. We get then the group velocity is equal to the spped of the particle.

v_particle = pc²/E = dE/dp = dω/dk = v_group

Since the phase velocity is v_ph = ω/k, then v_group = dω/dk = v_ph + k dv_ph/dk
If v_ph depends on k, v_ph = v_ph(k) is called dispersion relation. In this case the medium where the wave propagates is called dispersive such as water. the group velocity is greater thanj the phase velocity. If v_ph does not depends on k, v_group = v_ph, and the medium where the wave propagates is called nondispersive such as vacuum for electromagnetic waves.