A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Fourier series & Fourier Transforms
1. Orthogonal and orthonormal functions
1.1. Definitions
Two functions φ1 and φ2
are orthogonal on an interval [a, b] if the
integral of their product is null. That is:
∫ φ1(x) φ2(x) dx = 0
on the interval [a, b]
These functions are orthonormal if:
∫ φ1(x) φ2(x) dx = 1
on the interval [a, b]
If they are not, we can force them to be so by introducing the
weight function w(x) as follows:
∫ w(x) φ1(x) φ2(x) dx = 1
on the interval [a, b]
A set of functions {φn}, where n is
an integer, is orthogonal on
the intereval [a, b] if:
∫ φn(x) φm(x) dx = 0
on the interval [a, b] for n ≠ m
A set of functions {φn}, where n is
an integer, is orthonormal on
the intereval [a, b] if:
∫ φn(x) φm(x) dx = 1
on the interval [a, b] for n = m
That is the set {φn} is
normalized to 1:
∫ φn(x) 2 dx = 1
The integral ∫ φn(x) 2 dx
is written as:
||φn(x)||2, and is called the
norm of the function φn. This norm is
different from 1 in the case of the set is not normalized to 1.
1.2. Examples
1.2.1. Example 1
The tho following functions are orthogonal on the interval [-2, + 2]
φ1(x) = x
φ2(x) = x2
Indeed:
∫ φ1(x) φ2(x) dx =
∫ x. x2 dx = ∫ x3 dx =
x4/4 [-2, + 2] = 0
The set (p/π)(1/2) {cos nπx/p, sin mπx/p}
is orthonormal on the interval [- π + π];
The numbers "n" and "m" are integers,
and "p" is real.
Indeed:
For orthogonality:
∫ cos nπx/p cos mπx/p dx = 0 (E1)
∫ sin nπx/p sin mπx/p dx = 0 (E2)
∫ cos nπx/p sin mπx/p dx = 0 (E3)
For normality:
∫ cos2 nπx/p dx = p (E4)
∫ sin2 nπx/p dx = p (E5)
Proof:
We know:
cos (a + b) = cos a cos b - sin a sin b (1)
cos (a - b) = cos a cos b + sin a sin b (2)
sin (a + b) = sin a cos b + cos a sin b (3)
sin (a - b) = sin a cos b - cos a sin b (4)
Adding (1) and (2) gives:
cos a cos b = [cos (a + b) + cos (a - b)]/2
Subtracting (2) and (1) gives:
sin a sin b = [cos (a - b) - cos (a + b)]/2
Adding (3) and (4) gives:
sin a cos b = [sin (a + b) + sin (a - b)]/2
Setting a = b in (1) gives:
cos (2a) = cos2 a - sin2 a =
cos2 a - [1 - cos2 a] =
2 cos2 a - 1. Then:
cos2 a = [1 + cos (2a)]/2
And:
sin2 a = 1 - cos2 a =
1 - [1 + cos (2a)]/2 = [1 - cos (2a)]/2
1.
∫ cos nπx/p cos mπx/p dx =
∫ [cos (π/p)(n + m)x + cos (π/p)(n - m)x]/2 dx =
(1/2) ∫ [cos (π/p)(n + m)x] + (1/2) ∫ cos (π/p)(n - m)x] dx =
(1/2) (p/π(n + m)) [sin(π/p)(n + m)x] +
(1/2) p/π(n - m) [sin(π/p)(n - m)x].
Integration on [- p, + p] yields:
(1/2) (p/π) { [ sin π(n + m)]/(n + m) + [sin π(n + m)]/(n + m) +
[sin π(n - m)]/(n - m) + [sin π(n - m)]/(n - m)} =
(1/2) (p/ π) {2[sin π(n + m)]/(n + m) + 2[sin π(n - m)]/(n - m)} = 0
The equation (E1) is proved.
In the case of n = m, the first term is 0, and the second term
to 2 as: (sin x)/x tends to 1, we have [sin π(n - m)]/(n - m)} =
π [sin π(n - m)]/π(n - m)} tends to π and then:
∫ cos2 nπx/p dx = p
The equation (E4) is proved.
The set (1/p)1/2 { cos nπx/p, sin mπx/p } is normalozed to 1.
2.
∫ sin nπx/p sin mπx/p dx =
∫ [cos (π/p)(n - m)x - (π/p)cos (n + m)x]/2 dx =
(1/2) (p/π(n - m)) [sin(π/p)(n - m)x] -
(1/2) p/π(n + m) [sin(π/p)(n + m)x].
Integration on [- p, + p] yields:
(1/2) (p/ π) {[sin π(n - m)]/(n - m) +
[sin π(n - m)]/(n - m)
- [sin π(n + m)]/(n + m) - [sin π(n + m)]/(n + m)} =
(1/2) (p/ π) {2[sin π(n - m)]/(n - m)} =
(p/ π) {[ sin π(n - m)]/(n - m)} = 0
The equation (E2) is proved.
In the cas of n = m, since (sin x)/x tends to 1, we have:
∫ sin2 nπx/p dx = p
The equation (E5) is then proved.
3.
∫ cos nπx/p sin mπx/p dx =
(1/2) {∫ sin (n + m)πx/p + sin (n - m)πx/p dx} =
(1/2) {- ( p/(n + m)π) cos (n + m)πx/p -
( p/(n + m)π) cos (n - m)πx/p } =
- (p/π)(1/2) { [cos (n + m)πx/p ]/(n + m) -
[cos (n - m)πx/p]/(n + m)}.
Integration on [- p, + p] yields:
∫ cos nπx/p sin mπx/p dx =
- (p/π)(1/2) { [cos (n + m)π]/(n + m) -
cos (n + m)π]/(n + m)
- [cos (n - m)π]/(n + m) - [cos (n - m)π]/(n + m)} = 0.
The equation (E3) is then proved.
2. Fourier series
2.1. Definition
Is it possible to extend any function f defined on the interval [a, b] in
series of the orthonormal set {φn}?; that is:
f(x) = ∑ cn φn (x) n: 0 → ∞.
The response is yes. Here is the proof:
Integrating f(x) φm (x) from - a to + b yields:
∫ f(x) φm (x) dx = ∫ ∑ cn φn (x) φm (x) dx =
∑ cn ∫ φn (x) φm (x) dx
Since the set is orthonormal, the integral of the product ∫ φn (x) φm (x) is 0
for n ≠ m and 1 if n = m. Hence:
∑ cn ∫ φn (x) φm (x) dx =
cn ∫ φn2 (x) dx = cn || φn2 (x)||. Therefore:
cn = ∫f(x)φn(x)dx/||φn(x)||2
n : 0 → ∞ and x : a → b.
2.2. Particular case: Fourier series
Let's take the orthonormal set (p/π)(1/2) {cos nπx/p,
sin mπx/p} on the interval [- π + π].
Any function f defined on the interval [- p, + p] can be expended as:
f(x) = ∑ an cos nπx/p + bn sin mπx/p
n: 0 → ∞.
with: an = ∫f(x) cos nπx/p dx/||cos2 nπx/p(x)|| = ∫f(x) cos nπx/p dx/(p), and
bn = ∫f(x) sin nπx/p dx/||sin2 nπx/p(x)|| = ∫f(x) sin nπx/p dx/(p)
f(x) = ∑ an cos nπx/p + bn sin mπx/p
With the following coefficients:
an = (1/p) ∫f(x) cos nπx/p dx, and
bn = (1/p) ∫f(x) sin nπx/p dx
n : 0 → ∞, and x : - p → + p.
Particular cases:
If the function f is even, that is f(- x) = f(x),
then the product f(x) cos nπx/p is also
even, and f(x) sin nπx/p is odd; therefore:
an = (2/p) ∫f(x) cos nπx/p dx, and
bn = (1/p) ∫f(x) sin nπx/p dx = 0
n : 0 → ∞, and x : 0 → + p.
Hence:
f(x) = ∑ an cos nπx/p
If the function f is odd, that is f(- x) = - f(x),
then the product f(x) cos nπx/p is also
odd, and f(x) sin nπx/p is even; therefore:
an = (1/p) ∫f(x) cos nπx/p dx = 0 , and
bn = (2/p) ∫f(x) sin nπx/p dx
n : 0 → ∞, and x : 0 → + p.
Hence:
f(x) = ∑ bn sin nπx/p
To recap:
f is even:
f(x) = ∑ an cos nπx/p, with:
an = (2/p) ∫f(x) cos nπx/p dx
n : 0 → ∞, and x : 0 → + p.
That is the cosine series.
f is odd:
f(x) = ∑ bn sin nπx/p, with:
bn = (2/p) ∫f(x) sin nπx/p dx
n : 0 → ∞, and x : 0 → + p.
That is the sine series.
2. Complex Fourier series
We know that cos x = [eix + e- ix]/2, and
sin x = [eix - e- ix]/2i
Substituting these expressions in Fourier series of the function f
defined on the interval [- p, + p] yields:
f(x) = ∑ an cos nπx/p + bn sin mπx/p =
(1/2) ∑ an [einπx/p + e- inπx/p]
- i bn [einπx/p - e- inπx/p] =
(1/2) ∑ [an - i bn] einπx/p +
[an + i bn] e- inπx/p] =
∑ cn einπx/p + c- n e- inπx/p
Therefore:
f(x) = ∑ cn einπx/p + c-n e- inπx/p
With:
cn = [an - i bn]/2, and its conjugate:
c- n = [an + i bn]/2
The expressions of cn and c- n are found as follows:
I = ∫ f(x) e -imπx/p dx = ∑ cn ∫ ei(n - m)πx/p dx +
c- n ∫ e- i(n + m)πx/p dx
x : - p → +p
I = ∑ cn (p/i(n - m)π) [ei(n - m)π - e- i(n - m)π ] +
c- n (ip/(n + m)π) [e- i(n + m)π - ei(n + m)π] =
∑ cn (2p/(n - m)π) [sin ((n - m)π)] - c- n ( - 2 p/(n + m)π) [sin((n + m)π)] =
0 if n≠ m.
If n = m , we have, according to (sin x)/x = 1 when x tends to 0:
I = cn (2p) - c- n ( - p/n )π) [sin((2n)π)] = cn (2p) + 0 =
2p cn
Therefore:
cn = (1/2p) ∫ f(x) e- inπx/p dx
Similarly,
J = ∫ f(x) e+ imπx/p dx = ∑ cn ∫ ei(n + m)πx/p dx +
c- n ∫ e- i(n - m)πx/p dx
x : - p → +p
J = ∑ cn (p/i(n + m)π) [ei(n + m)π - e- i(n + m)π ] +
c- n (ip/(n - m)π) [e- i(n - m)π - ei(n - m)π] =
∑ cn (2p/(n + m)π [sin ((n + m)π)] - c- n ( - 2 p/(n - m)π) [sin((n - m)π)] =
0 if n≠ m.
If n = m , we have, according to (sin x)/x = 1 when x tends to 0:
J = cn (2p/2n)π [sin ((2n)π)] - c- n ( - 2p) = 0 + 2p c- n
Therefore:
c-n = (1/2p) ∫ f(x) e+ inπx/p dx
We recap as follows:
f is any function defined on the interval [- p, + p]
f(x) = ∑ cn einπx/p + c-n e- inπx/p
With the coefficients:
cn = (1/2p) ∫ f(x) e - inπx/p dx, and
c-n = (1/2p) ∫ f(x) e + inπx/p dx
n : 0 → ∞, and x : - p → + p.
Remark that, here, the number "n" can be negative as
well. So we can write:
f is any function defined on the interval [- p, + p]
f(x) = ∑ cn exp{ i(nπ/p)x }
With the coefficient:
cn = (1/2p) ∫ f(x) exp{ - i(nπ/p)x } dx,
n : - ∞ → + ∞, and x : - p → + p.
3. Fourier Transforms
We can write:
S = ∑ f(n) = ∑ f(n) 1 = ∑ f(n) [(n + 1) - n ] = ∑ f(n) dn,
therefore the sum S can be written as S = ∫ f(n) dn.
The above equations:
f(x) = ∑ cn exp{ i(nπ/p)x }
cn = (1/2p) ∫ f(x) exp{ - i(nπ/p)x } dx,
n : - ∞ → + ∞, and x : - p → + p.
can be then written as:
f(x) = ∫ c(n) exp{ i(nπ/p)x } dn
c(n) = (1/2p) ∫ f(x) exp{ - i(nπ/p)x } dx,
n : - ∞ → + ∞, and x : - p → + p.
let's change "n/p" into "x" and "πx" into "k"; with F(x) = p c(n), the
above equations become then:
f(k) = ∫ F(x) exp{ ikx} dx
F(x) = (1/2π) ∫ f(k) exp{ - ikx } dk,
x : - ∞ → + ∞, and k : - pπ → + pπ.
The number "p" is real. It can take the value ∞. We have then:
f(k) = ∫ F(x) exp{ ikx} dx
F(x) = (1/2π) ∫ f(k) exp{ - ikx } dk,
x : - ∞ → + ∞, and k : - ∞ → + ∞
F(x) is the Fourier Transform of f(k). f(k) is the
inverse transform of F(x).
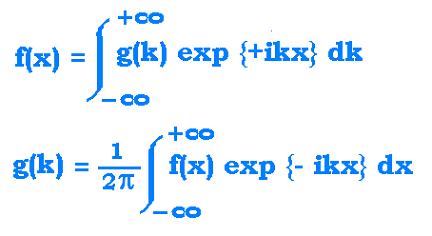
©: The scientificsentence.net. 2007.
|
|
|