A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Electromagnetic waves
1. The relationship E= cB
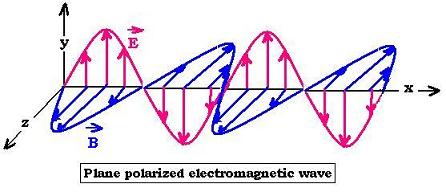
We have set that Maxwell's equations allow to set that light is an
electromagnetic wave. This wave is composed by an electric field and
magnetic field propagating together at the speed of light. These two
fields are transverse ans perpendicular to each other. We have
found the two wave equations for the fields E and B. This allow us
to write their expression as:
Ey = Eo sin (kEx - ωEt)
Bz = Bo sin (kBx - ωBt + φ)
We have seen the following equation:
∂Ey/∂x = - ∂Bz/∂t
By substituting in the expressions of E and B, we have:
Eo kE cos (kEx - ωEt) = ωB Bo cos (kBx - ωBt + φ)
This equation requires:
Eo kE = ωB Bo ,
kE = kB ,
ωE = ωB , and
φ = 0
We have finally:
Eo k cos (kx - ωt) = ω Bo cos (kx - ωt)
With ω = c k, we have:
Eo = c Bo
The expressions of E and B become:
Ey = Eo sin (kx - ωt)
Bz = Bo sin (kx - ωt)
2. Electromagnetic wave energy
An electromagnetic wave transports energy by the means of the
electric and magnetic fields. We know that the energy density
associated with the electric field is ue = (1/2) εo E2,
With magnetic field the density energy is um = (1/2μo) B2.
As the speed of light c = 1/[εoμo]1/2, and E = cB,
then εo = 1/μoc2 = B2/μoE2.
Thus: ue = (1/2) εo E2 = (1/2) B2/μoE2 E2
= B2/2μo = um.
The electromagnetic energy density is the sum :
uem = ue + um = 2 ue = εo E2
uem = εo E2
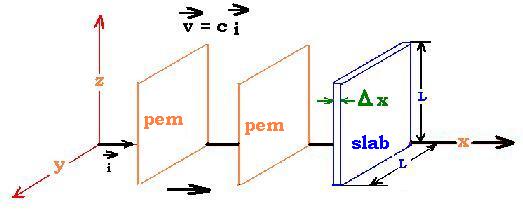
If the electromagnetic wave passes through a slab of volume Δx L2,
the energy density in this volume is U = uem Δx L2. The wave
travels at speed "c"; then the rate at which energy passes through the surface L2
of the slab perpendicular to the wave is:
U/Δt = U/(Δx/c) = Uc/Δx = c uem L2
The wave intensity is then: S = (U/Δt ) (1/L2) = c uem
We introduce the Poynting vector S = S i that
points in the propagation direction (over "x" axis) with the magnitude is
equal to the wave intensity:
S = (1/μo) E x B
(x is the cross product).
We use the average value of S, calculated as:
Sav = Average(S) = Average [(1/μo) EoBo sin2(kx - ωt)]
= (1/μo) EoBo (1/2) = EoBo /2μo
Sav = EoBo /2μo
©: The scientificsentence.net. 2007.
|
|
|