A sigle wave
Superposition of waves
© The scientific sentence. 2010
| Fraunhofer diffraction
1. Simple slit
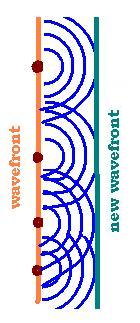
Huygens principle:
Each point on the wavefront is considered as a secondary
source of spherical wavelets.
A spherical wave generated at the aperture of width = b, at the position r = 0,
and time t = 0 propagates over the distance "r" till the point "P" on the screen. The
spaherical wave function at the point P is written as:
ψ(r,t)s = Ar exp{i(ωt - kr)}/r. The ampmlitude Ar
at the point "P" depends on the amplitude per unit volume Ao of the wave at the
origin r = 0 (at the aperture), and the geometry of the aperture g(r) = dS. So
ψ(r,t)s = Ao dS exp{i(ωt - kr)}/r
By considering the element dS, r gos from dS to the point P, we replace
then r by dS sin θ the wave function at the point P becomes:
ψ(r,t)s = Ao dS exp{i(ωt - kr - kSsinθ)}/r
Integrating the waves over the slit (between - b/2 and + b/2):
ψ(r,t)p = ∫ ψ(r,t)s dS
ψ(r,t)p = ∫ Ao dS exp{i(ωt - kr - kSsinθ)}/r =
Ao exp{i(ωt - kr}/r ∫ dS exp{- ikSsinθ)}
∫ dS exp{- ikSsinθ)} = (i/ksinθ) exp{- ikSsinθ)} [- b/2, + b/2]
We have:
exp{ikbsinθ)} - exp{- ikbsinθ)} = 2isin[kbsinθ)]. Then:
∫ dS exp{- ikSsinθ)} = (-2/ksinθ) sin[(1/2)kbsinθ)]
ψp(r,t) = Ao exp{i(ωt - kr}/r (2i/ksinθ) sin[(1/2)kbsinθ)] =
Ao (2i/ksinθ) sin[(1/2)kbsinθ)] exp{i(ωt - kr}/r
Let β = (1/2)kbsinθ, then:
ψp(r,t) = Ao (ib/β) sinβ exp{i(ωt - kr}/r
The wave we are working with is an electromagnetic wave, that is light.
The wave funtion is the electric field of the electromagnetic wave ψp(r,t)
= Ep = Eo (ib/β) sinβ exp{i(ωt - kr}/r. The related intensity is
I = (εoc/2) Ep2 = (εoc/2) EpEp*.
I = (εoc/2) [bEo/2]2 sin2β /β2.
That we can write:
I = Io sinc2β
sinc is the sine cardinal fuction: sinc(x) = sin(x)/x, and
Io = (εoc/2) [bEo/r]2
2. Rectangular aperture
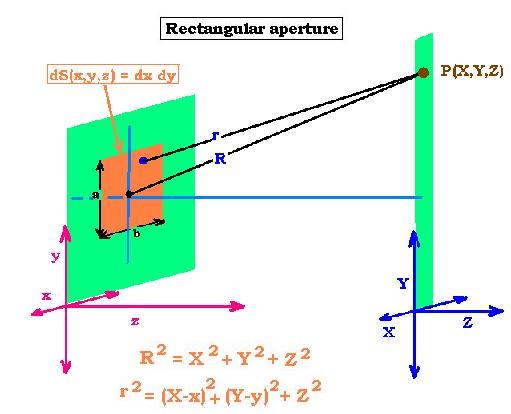
If Ao is now the amplitude per unit area, we can write again:
ψ(r,t)s = Ao dS exp{i(ωt - kr)}/r. Here dS is the
unit area dS = dx dy.
We have:
R2 = X2 + Y2 + Z2, and
r2 = (X - x)2 + (Y - y)2 + Z2
For the amplitude factor, r is close to R; regarding the distance slit-screen, but
it is not regarding the wavelength of the wave (light) in the phase factor . We can write:
ψ(r,t)s = (Ao dS/R) exp{i(ωt - kr)}.
r2 = (X - x)2 + (Y - y)2 + Z2 =
X2 + Y2 + Z2 + x2 + y2 - 2Xx - 2Yy
= R2 [1 + (x2 + y2)/R2 -2(Xx + Yy)/R2]
Then:
r = R [1 + (x2 + y2)/R2 -2(Xx + Yy)/R2]1/2
= R [1 + (x2 + y2)/2R2 - (Xx + Yy)/R2 + ... ]
Because of (x2 + y2)/R2 << 1, we have:
r = R [1 - (Xx + Yy)/R2 + ... ] ≈ R - (Xx + Yy)/R
The wave function becomes:
ψ(r,t)s = (Ao dS/R) exp{i(ωt - kR + k(Xx + Yy)/R)}
= Ao exp{i(ωt - kR)}/R) exp{ik(Xx + Yy)/R)} dS
ψ(r,t)s = (AodS/R) exp{i(ωt - kR)}) exp{ik(Xx + Yy)/R)}
ψ(r,t)p = ∫ ψ(r,t)s over the aperture [-a/2:+a/2 and -b/2:+a/2]=
ψ(r,t)p = Ao exp{i(ωt - kR)}/R) ∫exp{ik(Xx + Yy)/R)} dx dy
We have:
∫exp{ik(Xx + Yy)/R)} dx dy = ∫exp{ikXx /R)} dx ∫exp{ikYy/R)}dy =
(R/ikX)exp{ikXx /R)} (R/ikY)exp{ikXx /R)} =
(R/ikX)(R/ikY) [exp{ikXa/2R) - exp{-ikXa/2R) }][exp{ikXb/2R) - exp{-ikXb/2R) }] =
(R/ikX)(R/ikY) [2isin(kXa/2R)][2isin(kYb/2R)] =
= 4 (R/kX)(R/kY) [sin(kXa/2R)][sin(kYb/2R)]
ψ(r,t)p = 4 (R/YXk2) Ao exp{i(ωt - kR)}[sin(kXa/2R)][sin(kYb/2R)]
With:
sin θ = X/R
sin γ = Y/R
α = kasinθ/2
β = kbsinγ/2
Then:
ψ(r,t)p = 4 (R2/YXk2) (Ao/R) exp{i(ωt - kR)} sinα sinβ
= (a/α)(b/β)(Ao/R) exp{i(ωt - kR)} sinα sinβ
With a b = S,
ψ(r,t)p = (S Ao/R) exp{i(ωt - kR)} sincα sincβ
ψ(r,t)p = (S Ao/R) exp{i(ωt - kR)} sincα sincβ
I = (S Ao/R)2 sinc2α sinc2β =
I(X,Y) = Io sinc2α sinc2β
I(X,Y) = Io sinc2α sinc2β
3. Circular aperture
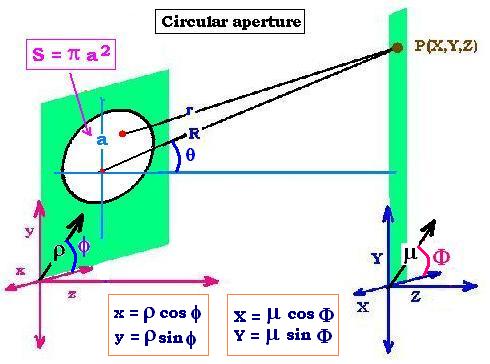
ψ(r,t)s = Ao dS exp{i(ωt - kr)}/r
ψ(r,t)p = ∫ ψ(r,t)s dS =
∫ ψ(r,t)s r dr dθ =
(Ao/R) exp{iωt} ∫ exp{- ikr)} r dr dθ =
(Ao/R) exp{iωt} ∫ exp{- ik(R - (Xx + Yy)/R)} r dr dθ
= (Ao/R) exp{iωt} ∫ exp{- ikR} exp{ik(Xx + Yy)/R} r dr dθ
exp{ik(Xx + Yy)/R} = exp{ik ρμ(cosφcosΦ + sinφsinΦ)/R}
cosφcosΦ + sinφsinΦ = cos(Φ - φ)
ψ(r,t)p =
(Ao/R) exp{i(ωt - kR)}
∫ exp{ik ρμcos(Φ - φ)/R} ρ dρ dφ
[ρ: 0 → a , φ: 0 → 2π]
This integrale is valid for any angle Φ in the screen, then for 0. We
The wave function becomes:
ψ(r,t)p =
(Ao/R) exp{i(ωt - kR)}
∫ ∫ exp{ik ρμ cos (φ)/R} ρ dρ dφ
[ρ: 0 → a , φ: 0 → 2π]
Using Bessel functions, we write:
∫ exp{i (kρμ/R) cosφ} dφ = 2π J0(kρμ/R)
Then:
∫ ∫ exp{ik ρμ cos (φ)/R} dφ ρ dρ = ∫ 2π J0(kρμ/R) ρ dρ
We have then:
ψ(r,t)p = 2π
(Ao/R) exp{i(ωt - kR)} ∫ J0(kρμ/R) ρ dρ
[ρ: 0 → a ]
Let: w = kρμ/R . Then ρ = (R/kμ)w and dρ = (R/kμ)dw
Then:
ψ(r,t)p = 2π (R/kμ)2
(Ao/R) exp{i(ωt - kR)} ∫ J0(w) w dw
[w: 0 → kaμ/R]
We have:
∫ J0(w) w dw = (kaμ/R) J1(kaμ/R) =
[w: 0 → kaμ/R ]
Then:
ψ(r,t)p = 2π (R/kμ)2
(Ao/R) exp{i(ωt - kR)} (kaμ/R) J1(kaμ/R)
ψ(r,t)p =
2π a2(Ao/R) exp{i(ωt - kR)} J1(kaμ/R) /(kaμ/R)
π a2 is the area of the aperture "S".
I = |ψ(r,t)p|2 =
Io [2 J1(kaμ/R) /(kaμ/R)]2
With: Io = S2 (Ao/R)2
Let sinθ = μ/R, then:
I(θ)= I(0) [2 J1(kasinθ) /(kasinθ)]2
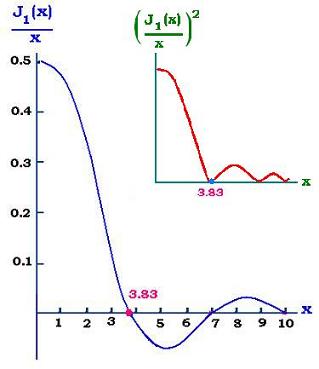
The first zero occurs at kaμ1/R = 3.83, that is 3.83/2π = aμ1/λR. Or
μ1 = 2(3.83/2π) λR /D where "D" is the diameter of the circular aperture.
μ1 = 2(3.83/2π) λR /D = (3.83/π) λR/D = 1.22 λR/D
μ1 = 2(3.83/2π) λR/D = 1.22 λR/D
Or:
sinθ = μ1/R = 1.22 λ/D
θ is generally small (D << R), hence sinθ = θ and:
θ = 1.22 λ/D
The result of shining a circular aperture by a monochromatic light is a diffraction pattern. The
first illuminated circular region (from 0 to3.83 in the plot of the intensity) is called Airy disk.
After, come a series of concentric bright rings which constitute the Airy pattern. If we have two light sources,
shining a circular aperture, their Airy disks will overlap. The criteriun to resolve two points objects
is the Rayleigh criterion , which says that two images are just resolved if the center of the central
maximum of one pattern falls on the first dark ring of the other.. In other words, to distinguish two object
sources in an image, the center of the central bright zone of one point source is located at the minimum of the other.
The relationship θR = 1.22 λ/D represents the limit of a resolution power for
an optical instrument. If Δθ(&theta1 - θ2) is the angle that represents the
separation of two objects is greater than θR, the itwo point sources are clearly resolved; if Δθ
is equal to θR, they are just resolved, and if Δθ is less than θR, they are
unresolved. This limit resolution is a physics fact that depends only of the diameter of its aperture and the
wavelength of the incident light. It is of great importance in telescopes and cameras .
©: The scientificsentence.net. 2007.
|
|
|