A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Jordan's lemma
1. Magnitude of an integral
If f(z) is a complex number, it can be written as:
∫ f(z) dz = r exp{i θ}
Then:
The real "r" can be expressed as:
r = |∫ f(z) dz|
r = Re [∫ exp{- i θ} f(z) dz] = ∫ Re [exp{- i θ} f(z) dz]
As Re(z) ≤ |z|, we have:
∫ Re [exp{- i θ} f(z) dz] ≤ ∫ |f(z) dz|
Therefore:
|∫ f(z) dz| ≤ ∫ |f(z)| dz
2. Jordan's lemma
Let the semicircle "C" in the upper half of the complex plan (x,y),
of radius "R" centered at the origin "o". The complex number z = x + i y is
represented as z = R exp{iθ}; then dz = i dθ R exp{iθ}. We
are interested in the following integral:
I(R) = ∫C exp {iaz} f(z) dz
f(z) is any function of the complex "z" that tends to zero as |z| = R tends to infinity.
The number "a" is real and positive. The argument of z arg z = θ lies in
the interval 0 ≤ arg z ≤ π as shown in the following figure:
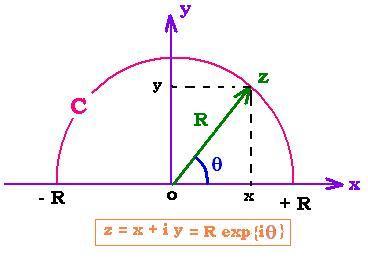
Let's rewrite I(R) in polar coordinates:
I(R) = i R ∫0 → π
exp {ia R cosθ - a R sinθ} f(R exp{iθ}) exp{iθ} dθ
If f(z) = f(R exp{iθ}) tends to 0 as R tends to ∞ it exist
a positive number ζ(R) that tends to 0 as R tends to ∞ such as:
|f(R exp{iθ})| < ζ(R). Therefore:
According to the property :
If f(z) = ∫ g(z) dz, then: |f(z)| < ∫ |g(z)| dz, we have:
|I(R)| < R ∫0 → π
|exp {ia R cosθ - a R sinθ} f(R exp{iθ}) exp{iθ}| dθ =
R ∫0 → π exp {- a R sinθ} |f(R exp{iθ})| dθ <
R ∫0 → π exp {- a R sinθ} ζ(R) dθ
Using the symetry of sinθ about θ = π/2, we have:
R ∫0 → π exp {- a R sinθ} ζ(R) dθ =
2 R ζ(R) ∫0 → π/2 exp {- a R sinθ} dθ
Then:
|I(R)| < 2 R ζ(R) ∫0 → π/2 exp {- a R sinθ} dθ
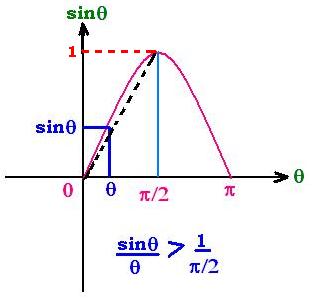
we have:
sin θ ≥ 2θ/π
sin θ = 2θ/π + b
Then:
∫0 → π/2 exp {- a R sinθ} dθ < =
exp {- a R b} ∫0 → π exp {- 2 a R θ/π} dθ =
∫0 → π/2 exp {- a R sinθ} dθ ≤
∫0 → π/2 exp {- 2 a R θ/π} dθ
Then:
|I(R)| < 2 R ζ(R) ∫0 → π/2 exp {- 2 a R θ/π} dθ
∫0 → π/2 exp {- 2 a R θ/π} dθ =
(1/ - 2 a R /π) [exp{- a R} - exp{0}] = (- π/ 2 a R ) [exp{- a R} - exp{0}] =
(π/2aR) [1 - exp{- a R}]
Thus:
∫0 → π/2 exp {- a R sinθ} dθ < ≤
(π/2aR) [1 - exp{- a R}]
And:
|I(R)| < 2 R ζ(R) (π/2aR) [1 - exp{- a R}] = ζ(R) (π/a) [1 - exp{- a R}]
When R → ∞ |I(R)| → 0 and I(R) → 0.
Let's write:
lim [R → ∞] ∫C exp {iaz} f(z) dz = 0
That is the Jordan's lemma.
© The scientific sentence. 2008.
|
|
|