Light is an electromagnetic wave
Wave equations for E and B
The Maxwell's equations in their integral forms are:
∮ E . dS = (1/ε0) Σqi
∮ B . dS = 0
∮ E dl = - d(∫B.dS)/dt
∮ B dl = μ0 ΣI + ε0 μ0 d(∫E.dS)/dt
These 1864 Maxwell's equations unify the electric and magnetic fiels. Their both
linked propagation predict the existence of an electromagnetic wave,
which Maxwell called light. At this time these equations describe the
behavior of visible light, radio waves, microwaves, and x-rays.
In the vacuum without any presence of a net charge or current (Σqi = 0 and
μ0 ΣI = 0) as in the cube in the figure, we have:
∮ E . dS = 0 (1)
∮ B . dS = 0 (2)
∮ E dl = - d(∫B.dS)/dt (3)
∮ B dl = ε0 μ0 d(∫E.dS)/dt
(4)
In this chapter, we will show that the description of an electromagnetic wave comes
from these equations.
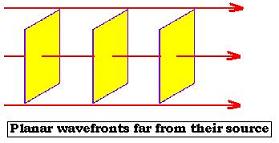 Let's consider that the wave is moving with respect to the "x" direction, and far from the charge
source (source of the waves), the wavefronts are planar (they are spherical near the source and
become planar far from the source) . This approximation is called the plane-wave approximation.
Therefore the fields E and B do not depend on the components "y" and "z";
Let's consider that the wave is moving with respect to the "x" direction, and far from the charge
source (source of the waves), the wavefronts are planar (they are spherical near the source and
become planar far from the source) . This approximation is called the plane-wave approximation.
Therefore the fields E and B do not depend on the components "y" and "z";
hence: E = E(x,t) and B = B(x,t).
1. E and B are transverse
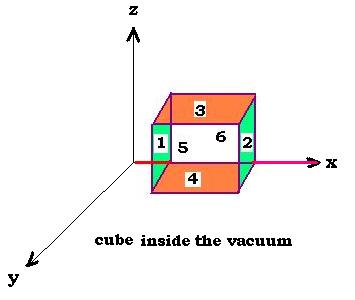
The gaussian surface is the surface of the cube composed by
the six faces 1,2,3,4,5, and 6. The Gauss law, for this cube is written
as follows:
∮ E . dS = 0 = ∫Ex(1)dS(1) + ∫Ex(2)dS(2) + ∫Ez(3)dS(3) +
∫Ez(4)dS(4) + ∫Ey(5)dS(5) + ∫Ey(6)dS(6) (1)
Where:
E(n) is the electric field that crosses the side "n", and dS(n) the elementary
surface vector of the side "n". We have:
dS(1) = - dS(2) = dz dy, dS(3) = - dS(4) = dy dx, and dS(5) = dS(6) = dx dz
Since the field E does not depend on "y" nor on "z", we have: Ey(5) = Ey(6),
Ez (3) = Ez (4), but Ex (1) is different from Ex (2).
Therefore, in the equation (1) the third term and the fourth terms cancel each other; the fifth and the sixth
terms as well.
The equation (1) becomes:
∫Ex(1)dz dy + ∫Ex(2)dz dy = 0
If we write: ∫ dz dy = Δz Δy, we have then Ex(1) = Ex(2); that is
Ex does not depend on "x". But E does depend on "x", that means
that the dependency on "x" exist on the components "y" and "z", as E = E(0, f(x), g(x));. If
Ex does not depend on x, that means Ex is constant the long of "x", even
when it is equal to zero. We have to conclude that Ex == 0. Forethermore the electric
field wave is transverse, it has no component along the direction of the propagation.
Similarly, by the same analysis using the relation (2), we conclude that the magnetic
field wave is transverse.
2. E and B are perpendicular
The wave propagates along "x". E and B are transverse ( E and B are
perpendicular to "x").
Now, let's oriente E along "y" and write E = Ey(x,t);
and determine the direction of B.
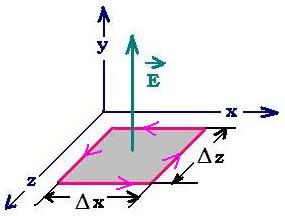
From the equations of Maxwell, we will use the fourth relationship, that is the Fraday's law.
∮ E dl = - d(∫B.dS)/dt
Let's consider the small square path in the plane (x,z) as shown in the
figure.
Each displacement along this path is perpendicular to the electric field E, we have
∮ E dl = 0. Thus d(∫B.dS)/dt = 0, with dS = dx dz.
The integration of the relationship d(∫B.dS)/dt gives: d/dt [By.ΔxΔz]. Hence:
ΔxΔz ∂By/∂t= 0. This result means that By does
not depend on t, but does the magnetic field B. Hence By is constant in time even
when B = 0. We conclude then By = 0.
Since Bx = 0 (from 1.1.), and By = 0; it remains only the "z" component.
We can write then: B = B(x,t) along the "z" axis.
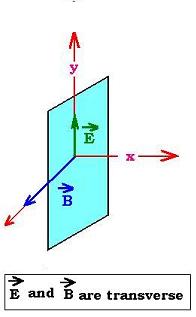
The conclusion is :
E = Ey(x,t); and B = Bz(x,t), then E and B are perpendicular. The wave
moves along "x". B ocsillates in the plane (x,z) and E oscillates in the plane (x,y) which
is the plane of polarization of the wave.
3. The wave equation for E and B
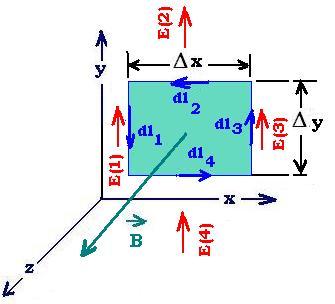
Now, we will apply again the Fraday's law for the following square path::
∮ E dl = - d(∫B.dS)/dt (equation 3)
The left-hand side of the Faraday's law is:
∮ E dl = ∫E(1)dl1 + ∫E(2)dl2 +
∫E(3)dl3 + ∫E(4)dl4 =
∫E(1)dl1 - ∫E(3)dl3 =
[- Ey(1) + Ey(3)]Δy = Δy Δx [- Ey(1) + Ey(3)]/Δx
= Δy Δx ∂ Ey/∂x
The right-hand side fo the Faraday's law is:
- d(∫B.dS)/dt = - Δy Δx ∂Bz/∂t
Then, the Faraday's law becomes:
Δy Δx ∂ Ey/∂x = - Δy Δx ∂Bz/∂t
Or:
∂Ey/∂x = - ∂Bz/∂t
(3.1)
Now, we will use the fourth equation:
∮ B dl = ε0 μ0 d(∫E.dS)/dt
Along the square path
∮ B dl = ∫B(1)dl1 + ∫B(2)dl2 +
∫B(3)dl3 + ∫B(4)dl4 =
∫B(1)dl1 - ∫B(3)dl3 =
[- Bz(1) + Bz(3)]Δy = Δy Δx [- Bz(1) + Bz(3)]/Δx
= Δy Δx ∂Bz/∂x
E dS = Ey Δy (- Δx) and d(∫Ey.dS)/dt = - Δy Δx dEy/dt
Equating, we get:
Δy Δx ∂ Bz/∂x = - ε0 μ0 Δy Δx ∂Ey/∂t
That is:
∂Bz/∂x = - ε0 μ0 ∂Ey/∂t
(3.2)
Differentiating the equations (3.1) and the equation (3.2) with respect to
x and t respectively, we find:
∂2Ey/∂x2 = - ∂[∂Bz/∂t]/∂x
∂[∂Bz/∂x]/∂t = - ε0 μ0 ∂2Ey/∂t2
Thus:
∂2Ey/∂x2 = ε0 μ0 ∂2Ey/∂t2
Similarly, if we differentiate the equations (3.1) and the equation (3.2) with respect to
t and x respectively, we find:
∂[∂Ey/∂x ]∂t = - ∂2Bz/∂t2
∂2Bz/∂x2 = - ε0 μ0 ∂[∂Ey/∂t]∂x
Thus:
∂2Bz/∂x2 = ε0 μ0 ∂2Bz/∂t2
These two equations are the wave equations for E and B. Comparing with the harmonic wave equation,
we can express the speed of the wave as 1/v2 = ε0 μ0. Hence:
v = c = [ε0 μ0]- 1/2
ε0 = 4π x 10- 7 kg.m/s2.A2
μ0 = 8.85 x 10- 12 s4. A2/kg.m3
Then:
c = 3.00 x 108 m/s. That is the speed of light in the vacuum.
As Maxwell did, we
proclame that, since the electromagnetic (E&B) wave propagates at the speed of light; then light
is an electromagnetic wave.
©: The scientificsentence.net. 2007.
|