A sigle wave
Superposition of waves
© The scientific sentence. 2010
|
Wave packets
1. Superposition of two waves
Supperposing two waves in phase of equal frequency and amplitude just
doubles the resultant amplitude; when they are out of phase, the two combined waves just cancel each other.
Supperposing two waves in phase of equal frequency and different amplitudes just
enlarge the resultant amplitude.
The most interesting is the supperposition of two or more waves of almost the same frequency
that corresponds to the beats phenomenon.
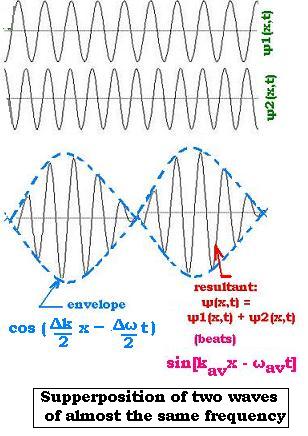
Let's consider the two following wave functions:
ψ1(x,t) = A sin(k1x - ω1t)
ψ2(x,t) = A sin(k2x - ω2t)
Which are waves traveling in the same direction with the same
amplitude A, different wave number k and different angular frequency ω .
We use the principle of superposition to find the resultant wave
ψ(x,t) = ψ1(x,t) + ψ2(x,t).
Then:
ψ(x,t) = A[sin(k1x - ω1t) + sin(k2x - ω2t)]
Using the trigonometric identity:
sin (a + b) + sin (a - b) = 2 sin a cos b;
With: a + b = x and a - b = y ,
we get: a = (x + y )/2 and b = (x - y)/2
Then:
sin (x) + sin (y) = 2 sin [(x + y )/2] cos [(x - y )/2]
It follows that:
ψ(x,t) = 2A sin ([k1x - ω1t + k2x - ω2t]/2)
cos([k1x - ω1t - k2x + ω2t]]/2)
= 2A sin [(1/2)(k1 + k2)x - (1/2)(ω1 + ω2)t]
cos[(1/2)(k1 - k2)x - (1/2)(ω1 - ω2)t]
Thus:
ψ(x,t) = 2A cos[(Δk/2)x - (Δω/2)t] sin[kavx - ωavt]
(1)
With:
Δk = k1 - k2
Δω = ω1 - ω2
kav = (k1 + k2)/2
ωav = (ω1 + ω2)/2
The factor cos[(Δk/2)x - (Δω/2)t] represents the envelope of the
combined waves. The resultant wave expressed by the factor sin[kavx - ωavt]
oscillates within the envelope with the wave number kav and angular frequency ωav.
Each individual wave moves with its own phase volocity ω1/k1 and
ω2/k2. The combined wave moves with the phase velocity ωav/kav.
The envelope which represents the pulse or the wave packet moves at the group velocity Δω/Δk.
2. Superposition of many waves: The wave packet
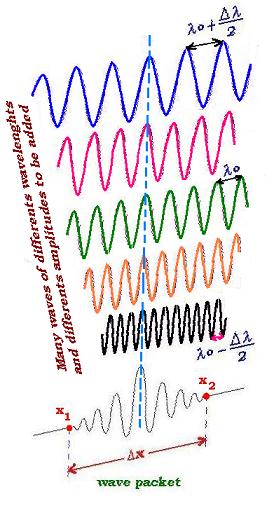
Combining many waves leads to a pulse or wave packet as for combining two waves. But the
more we add waves the more the distance between the pulses becomes larger; and for a given time
we can see less wave-packet pass through the direction of the propagation. In other words, a
finite number of different monochromatic waves always produce infinite sequence of repeating
pulses (wave groups). As we want to localize the packet, we need to stabilize
the packet, we will then add an infinite number of waves with a particular well chosen amplitude.
The effective idea is to fix a wave number ko and let the envelope takes effect
about this centred wave number ko (or wavelength λo). The Gaussian
is the appropriate example. It plays the role of having constructive interference over the space-time
and destructive interference elsewhere.
The wave function of the wave-packet can then be written as:
ψ(x,t) = ∑ ψi(x,t) = ∑ A sin(kix - ωit)
Or, with different amplitudes:
ψ(x,t) = ∑ Ai sin(kix - ωit) (2)
Wich is called Fourier series.
When dealing with a continuous spectrum, the Fourier series bocome the
Fourier integral:
ψ(x,t) = ∫A(k) sin(kx - ωt) dk (3)
k: - ∞ → + ∞
If Δx is the space where we can localize the packet-wave, |ψ(x,t)|2dx is
the probability of finding the wave-packet within Δx. If Δk is the range around ko
that is set to form a wave packet, and Δx the region between the two consecutive
points where the envelope is zero (Δx = x2 - x1); we can write from the relationship (1):
cos[(Δk/2)x1 - (Δω/2)t] = 0; and cos[(Δk/2)x2 - (Δω/2)t] = 0.
We can write: (Δk/2)x1 - (Δω/2)t = π/2,
and (Δk/2)x1 - (Δω/2)t = 3π/2.
We have then:
(Δk/2)x2 - (Δω/2)t - (Δk/2)x1 + (Δω/2)t = π.
That is: (Δk/2)(x2 - x1) = π, which is called:
The uncertainty principle:
Δk Δx = 2π (4)
Contrary to the Classical Mechanics that allows both the measure of the position and the momentum
of a particle at a certain same time, Wave Mechanics allows just one, the other is uncertain.
The above relation is set for the combination of two waves. It is not very precise.
It tells us just in order to know precisely the position of the wave packet (or to
localize a particle), then Δx small, we need a large range of wave numbers (Δk large).
With ω = 2π ν, and k = 2π/λ = 2πν/v, and x = vt(ν is the frequency,
v the velocity, and x the displacement of the particle), the above relation becomes
Δω Δt = 2π. This relationship tells us also that to know precily (at a
fixed small time) when the packet is located at a given point, we need a large range of frequencies ω.
It has an important role in Electronis. It shows that the bandwidth must be large of a circuit to send
a signal in a short time (a dial-up Internet connection works with a very narrow bandwidth about 50 Kbps
(Kilo bits per second), whereas, a broadband connection can let move a large amount of data at about
some Mbps (Mega bits per second).
3. Matter-wave concept
The de Broglie relationship set the wave-particle duality. Further, the description of matter
particle by a wave packet is justifed by the fact they move at the same velocity. Indeed, the
the wave-packet moves at the speed of the envelope called the group velocity vg
equal to Δω/Δk = dω/dk. This derivative is set about the most probable value
of k that is ko.
If a particle (relativistic) has the total energy E, E2
= p2c2 + m2c4, its mass m = m(v) = γm with
γ = 1/[1 - v2/c2]1/2, its impulsion p = γmv. With
E = m(v)c2 = γmc2, we have E2v2/c2 = p2c2,
then v = pc2/E.
But the derivative of the relationship E2 = p2c2 + m2c4
gives: 2EdE = 2c2pdp, that is pc2/E = dE/dP.
Using dE/dP = d(hω/2π)/d(hk/2π) = dω/dk. We get then the group velocity is equal to
the spped of the particle.
vparticle = pc2/E = dE/dp = dω/dk = vgroup
Since the phase velocity is vph = ω/k, then
vgroup = dω/dk = vph + k dvph/dk
If vph depends on k, vph = vph(k) is called dispersion relation. In this
case the medium where the wave propagates is called dispersive such as water. the group velocity is greater thanj
the phase velocity. If vph does not depends on k, vgroup = vph, and
the medium where the wave propagates is called nondispersive such as vacuum for
electromagnetic waves.
©: The scientificsentence.net. 2007.
|
|
|