Expressions of traveling waves

1. Spherical wave expression

We know that the Laplacian in spherical coordinates is written as :
Δ = ∂²/∂r² + (2/r)∂/∂r

The equation of propagation of the wave ψ(r,t) is:
Δ ψ(r,t) - (1/v²)∂²ψ(r,t)/∂t² = 0
That is, in "r" spherical coordinates component:
∂²ψ(r,t)/∂r² + (2/r)∂ψ(r,t)/∂r - (1/v²)∂²ψ(r,t)/∂t² = 0

Rearranging, this equation becomes:
∂²[rψ(r,t)]/∂r² - (1/v²)∂²[rψ(r,t)]/∂t² = 0

If φ(r,t) is the solution of the equation:
Δφ(r,t) - (1/v²)∂²φ(r,t)/∂t² = 0
Then The solution for the equation:
∂²[rψ(r,t)]/∂r² - (1/v²)∂²[rψ(r,t)]/∂t² = 0
is: ψ(r,t) = φ(r,t)/r, which represents a spherical wave .

Example:
For a harmonic wave: φ(r,t) = φ(x,t) = A sin(kx - ωt). Thus:
ψ(r,t) = φ(r,t)/r = φ(x,t)/r = A sin(kx - ωt)/r

If the epxression of the wave is complex and written as: φ(r,t) = φ(x,t) = A exp {i(kx - ωt)}. Then: ψ(r,t) = φ(r,t)/r = φ(x,t)/r = A exp {i(kx - ωt)}/r

2. Plane wave expression

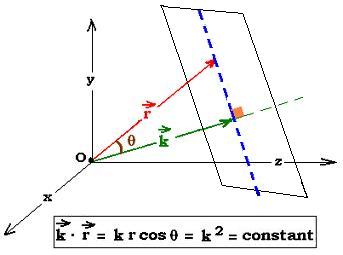
The general expression of a plane wave is:
w(z,t) = w_o cos(ωt - kz)
w_o is the amplitude, ω is the frequency, and k is the wave number of the wave traveling along the axis "z". This wave oscillates in the plane "yz". In three dimension space, "k" is a vector of components k_x, k_y, and k_z. If "r" is the position vector and "k" is the wave vector, pointing in any direction in space, the plane wave will take the folowing expression:

w(r,t) = w_o cos(ωt - kr)

For every plan perpendicular to the direction of the propagation of the traveling wave (along the wave vector k), the dot product k.r is constant, therefore w(r,t) is the same.. At a certain fixed time, the wave traveling along "k" have the same value in every plan perpendicular to the direction of propagation. The wavefronts are planar and thus the wave is a plane wave.

Remark:
The expression of a plane wave can also be written in complex form:

w(r,t) = w_o exp i{ωt - kr}
That allows calculus to become easier do and take thereafter the real part of the final searched exression.